手动置顶：特殊的行列式计算

• Laplace定理！
  设D是n阶行列式，在D中任取k行(列)，再取所有的k列(行)，D=∑（交叉元素方阵的行列式 × 这k行k列的代数余子式）
• Vandermonder行列式 $$V_{n}=\left|\begin{array}{lllll} 1 & 1 & \cdots & 1 & 1 \\ x_{1} & x_{2} & \cdots & x_{n-1} & x_{n} \\ x_{1}^{2} & x_{2}^{2} & \cdots & x_{n-1}^{2} & x_{n}^{2} \\ \vdots & \vdots & & \vdots & \vdots \\ x_{1}^{n-2} & x_{2}^{n-2} & \cdots & x_{n-1}^{n-2} & x_{n}^{n-2} \\ x_{1}^{n-1} & x_{2}^{n-1} & \cdots & x_{n-1}^{n-1} & x_{n}^{n-1} \end{array}\right|$$

$$V_{n}=\prod_{1 \leq i<j \leq n}\left(x_{j}-x_{i}\right)$$

• 爪形行列式

  $$D=\left|\begin{array}{lllll} a_{0} & a_{1} & a_{2} & \cdots & a_{n} \\ b_{1} & d_{1} & 0 & \cdots & 0 \\ b_{2} & 0 & d_{2} & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ b_{n} & 0 & 0 & \cdots & d_{n} \end{array}\right|$$

  如果主对角线上元素 $d_{k}$ 均不为零, 则可将 $d_{k}$ 所在的列的 $-\frac{b_{k}}{d_{k}}$ 倍加到第一列，就将行列式化为上三角行列式:

  $$\begin{array}{l} D & =\left|\begin{array}{ccccc} a_{0}-\sum_{k=1}^{n}\frac{a_{k} b_{k}}{d_{k}} & a_{1} & a_{2} & \cdots & a_{n} \\ 0 & d_{1} & 0 & \cdots & 0 \\ 0 & 0 & d_{2} & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & d_{n} \end{array}\right| \\ & =\left(a_{0}-\sum_{k=1}^{n} \frac{a_{k} b_{k}}{d_{k}}\right) d_{1} d_{2} \cdots d_{n} \end{array}$$

• 三对角行列式

  • 简化情况 $$D_{n}=\left|\begin{array}{cccccc} b & c & & & & & \\ a & b & c & & & & \\ & a & b & c & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & a & b & c & \\ & & & & a & b & c \\ & & & & & a & b \end{array}\right|$$ $$\text{令}\left\{\begin{array}{l} x=\frac{b-\sqrt{b^{2}-4 a c}}{2} \\ y=\frac{b+\sqrt{b^{2}-4 a c}}{2} \end{array}\right.$$ $$D_{n}=\left\{\begin{array}{l} \frac{y^{n+1}-x^{n+1}}{y-x}, x \neq y\left(b^{2}-4 a c>0\right) \\ (n+1) x^{n}, x=y\left(b^{2}-4 a c=0\right) \end{array}\right.$$
  • 完整情况 $$D_{n}=\left|\begin{array}{cccccc} \alpha_{1} & \beta_{1} & & & & & \\ \gamma_{1} & \alpha_{2} & \beta_{2} & & & & \\ & \gamma_{2} & \alpha_{3} & \beta_{3} & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & \gamma_{n-3} & \alpha_{n-2} & \beta_{n-2} & \\ & & & & \gamma_{n-2} & \alpha_{n-1} & \beta_{n-1} \\ & & & & & \gamma_{n-1} & \alpha_{n} \end{array}\right|$$ $$|D_n|=\alpha_{n} |D_{n-1}|-\beta_{n-1} \gamma_{n-1} |D_{n-2}|$$
• 除对角线外元素全相等的行列式：
  

第一章 线性方程组与矩阵

零矩阵

单位矩阵

行矩阵和列矩阵

对角矩阵

• 对角矩阵的性质
  • 同阶对角矩阵的乘积仍为对角阵，且它们的乘积是可交换的
    
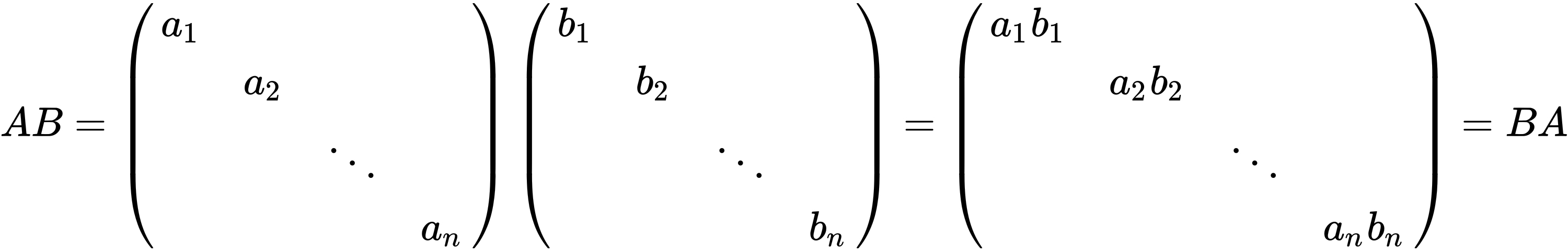
  • 对角矩阵的n次方即计算每个元素的n次方

上三角矩阵

• 上三角矩阵的乘积还是上三角矩阵
• 可逆的上三角矩阵A之逆仍为上三角矩阵
  • 证明：对矩阵A的阶数用数学归纳法。当n=1时，结论显然
    假设结论对n-1阶矩阵成立，记 $$A=\left(\begin{array}{cc} a_{11} & \alpha^{T} \\ \mathbf{0} & A_{n-1} \end{array}\right)$$ 由A可逆知$a_{11} \neq 0$及$A_{n-1}$可逆, 于是 $$A^{-1}=\left(\begin{array}{cc} a_{11}^{-1} & -a_{11}^{-1} \alpha^{T} A_{n-1}^{-1} \\ 0 & A_{n-1}^{-1} \end{array}\right)$$ 由归纳假设知$A_{n-1}^{-1}$是上三角矩阵, 所以$A^{-1}$也是上三角矩阵

矩阵的初等行变换

阶梯形矩阵

简化阶梯形（规范阶梯形、Hermite）

第二章 矩阵

矩阵加减、数乘

加法交换律

加法结合律

矩阵乘法

乘法结合律

乘法分配律

性质

• 两个同阶上三角矩阵的乘积还是上三角矩阵
• 矩阵乘法有零因子，即存在矩阵$A\ne O$, $B\ne O$, 且$AB=O$

相乘可换

• 若A、B相乘可换，则A、B必是同阶方阵
• 单位矩阵与任何与之同阶的方阵相乘可换
• 数量矩阵同与之同阶的方阵相乘可换
• 同阶对角矩阵相乘可换

方阵的幂

对称矩阵与反对称矩阵

• $A$是反对称矩阵$\Leftrightarrow$ $\forall $列矩阵 $\alpha:\alpha^TA\alpha=0$
• 任一$n$阶方阵$A$都可以表示成对称矩阵和反对称矩阵之和
  $A=\frac{1}{2}\left(A+A^{T}\right)+\frac{1}{2}\left(A-A^{T}\right)$

转置矩阵

• 转置矩阵的性质
  • $ (A^T)^T=A$
  • $ (B+C)^T=B^T+C^T$
  • $ (kA)^T=kA^T$
  • $(AB)^T=B^TA^T$
  • 若$A$为方阵，则$(A^m)^T=(A^T)^m$，$m$为正整数
  • $ A$为对称矩阵$\leftrightarrow A^T=A$，$A$为反对称矩阵$\leftrightarrow A^T=-A$
  • $|A^T|=|A|$
  • 实矩阵$A_{m×n},tr(AA^T)=0$，求证$A=0$
  • 方阵$A_n$满足$A^2=AA^T$，求证$A$是实对称矩阵

方阵的迹

• 性质
  • $\operatorname{tr}(\boldsymbol{A}+\boldsymbol{B})=\operatorname{tr}(\boldsymbol{A})+\operatorname{tr}(\boldsymbol{B})$
  • $\operatorname{tr}(k\boldsymbol{A})=k\operatorname{tr}(\boldsymbol{A})$
  • $\operatorname{tr}(\boldsymbol{A}\boldsymbol{B})=\operatorname{tr}(\boldsymbol{B}\boldsymbol{A})$
  • $\operatorname{tr}(\boldsymbol{A}^T)=\operatorname{tr}(\boldsymbol{A})$
  • $\operatorname{tr}(\boldsymbol{AA}^\mathrm{T})=\operatorname{tr}(\boldsymbol{A}^\mathrm{T}\boldsymbol{A})$
  • 若 $\operatorname{tr}(\boldsymbol{AA}^\mathrm{T})=0$ ，则 $\boldsymbol{A}=\mathbf{0}$

行列式的性质

• $|A^T|=|A|$
• 行列式不等于零的矩阵又称为非奇异矩阵
• 交换行列式中两行的位置，行列式变号
• 把行列式的某一行的所有元素同乘以数c，等于用数c乘以这个行列式
• 如果行列式某一行的各元素都是两个元素之和，则这个行列式等于两个行列式之和
• 如果把行列式某一行的各元素都同乘以数k再加到另一行的对应元素上去，则行列式的值不变
• 如果$A、B$是同阶方阵，$|AB|=|A||B|$
• $\left|A^n\right|=\left|A\right|^n$
• $|kA|=k^n|A|$
• 对角矩阵的行列式=对角线元素积
• 反对角矩阵的行列式=反对角线元素积再乘$(-1)^{\frac{n(n-1)}{2}}$
• 行列式中某行的所有元素都是两个元素的和，则此行列式可分解为两个行列式的和，即
• $$\left|\begin{array}{ccc} a_{11} & \cdots & a_{1 n} \\ \vdots & & \vdots \\ a_{i 1}+b_{1} & \cdots & a_{i n}+b_{n} \\ \vdots & & \vdots \\ a_{n 1} & \cdots & a_{n n} \end{array}\right|=\left|\begin{array}{ccc} a_{11} & \cdots & a_{1 n} \\ \vdots & & \vdots \\ a_{i 1} & \cdots & a_{i n} \\ \vdots & & \vdots \\ a_{n 1} & \cdots & a_{n n} \end{array}\right|+\left|\begin{array}{ccc} a_{11} & \cdots & a_{1 n} \\ \vdots & & \vdots \\ b_{1} & \cdots & b_{n} \\ \vdots & & \vdots \\ a_{n 1} & \cdots & a_{n n} \end{array}\right|$$

余子式和代数余子式

• 定义：略
• 性质
  • $n$阶行列式$D=|a_{ij}|_n$等于它的任一行的所有元素与它们各自的代数余子式的乘积之和
  • 用一个行列式某一行(列)乘以别人的代数余子式等于零

逆矩阵

• 定义：略（注意：只有方阵才有逆矩阵）
• 性质
  • 逆矩阵通常被称为互逆矩阵
  • 若$A$有左逆$B$或有右逆$C$，则$A$可逆且$A^{-1} =B = C$
  • $A$可逆的充要条件是行列式不为$0$
  • $(A^{-1})^{-1}=A$
  • $(k A)^{-1}=\frac{1}{k} A^{-1}$
  • $(A B)^{-1}=B^{-1} A^{-1},\left(A_{1} A_{2} \cdots A_{s}\right)^{-1}=A_{s}^{-1} \cdots A_{2}^{-1} A_{1}^{-1}$
  • $\left(A^{T}\right)^{-1}=\left(A^{-1}\right)^{T}$
  • $\left|A^{-1}\right|=|A|^{-1}$
  • $\left(A^{s}\right)^{-1}=\left(A^{-1}\right)^{s}$
  • 设$A$为$n$阶矩阵，且$A^k=O$，求证$(E-A)^{-1}=E+A+A^2+\cdots+A^{k-1}$
  • 三角矩阵的逆矩阵仍然是三角矩阵
  • $AB=AC$可消去$A$的充要条件是$A$可逆
• 一种逆矩阵+矩阵乘法的简便计算方法
  

伴随矩阵

• 定义：略（注意$A_{ij}$在$(j,i)$位置）
• 定理：$AA^{*}=A^{*}A=|A|E$
• 性质
  • $(AB)^{*}=B^{*}A^{*}$
  • $|A^{*}|=|A|^{n-1}$
  • $A^{-1}=|A|^{-1}A^{*}$
  • $(A^{-1})^{*}=(A^{*})^{-1}$
  • $(A^{T})^{*}=(A^{*})^{T}$
  • $A^{**}=|A|^{(n-2)}A$

分块矩阵

• 定义：一般的，对$m×n$矩阵$A$，若先用若干条横线把它分成$r$个条，再用若干条竖线把它分成若干竖条，然后把每一块上的小矩阵当成一个元素看待，就得到了分块矩阵
• 分块矩阵的运算
  • 加法：要求行列数相同，采用相同的分块法（同阶分块矩阵）
  • 数乘：略
  • 矩阵乘法：略
  • 转置：整个转置+子矩阵转置
  • 共轭：每个元素共轭
• 分块矩阵的初等变换
  • 第一类：对调分块矩阵中某两块行(列)的位置；
  • 第二类：用可逆矩阵左乘分块矩阵的某一块行，或右乘某一块列；
  • 第三类：用某一矩阵左乘分块矩阵的某一块行后加到另一行块上去，或右乘某一块列后加到另一块列上去
  • 第三类块初等变换不改变矩阵的行列式
• 分块初等矩阵：设$E=diag\{E_1,\cdots,E_k\}$（单位矩阵的分块对角矩阵），则用三类块的初等变换作用于E得到三类分块初等矩阵
  • 对分块矩阵作初等行(列)变换，等于在其左(右)边乘以相应的分块初等矩阵
  • 例：$A$是$n\times n$方阵，$\alpha_i$是$n$行 列向量，求证：$A(\alpha_1,\alpha_2,\cdots,\alpha_n)=(A\alpha_1,A\alpha_2,\cdots,A\alpha_n)$

第一降阶公式

• 当A可逆时 $$\left|\begin{array}{cc} A & B \\ C & D \end{array}\right|=\left|\begin{array}{cc} A & B \\ O & D-C A^{-1} B \end{array}\right|=|A|\left|D-C A^{-1} B\right|$$
• 当D可逆时 $$\left|\begin{array}{cc} A & B \\ C & D \end{array}\right|=\left|\begin{array}{cc} A-B D^{-1} C & B \\ O & D \end{array}\right|=\left|D \| A-B D^{-1} C\right|$$
• 当A和D都可逆时 $$|A|\left|D-C A^{-1} B\right|=|D||A-B D^{-1} C|$$

标准单位列向量：

$$\varepsilon_{j}=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{array}\right)$$

标准单位行向量：

$$\mathbf{e}_{i}=(0, \cdots, 0,1,0, \cdots, 0)$$

分块对角矩阵

• 定义： $$\operatorname{diag}\left(A_{1}, A_{2}, \cdots, A_{s}\right)=\left(\begin{array}{cccc} A_{1} & & & \\ & A_{2} & & \\ & & \ddots & \\ & & & A_{s} \end{array}\right)$$
• 性质：
  • 分块对角阵的行列式：对角线每个元素（要是方阵）行列式之积
  • 分块对角阵的逆矩阵：对角线每个元素取逆矩阵
  • 分块反对角阵的行列式：对角线每个元素行列式之积 × $(-1)^{\sum_{i<j}a_i×a_j}$（$a_k$表示子矩阵的阶数）
  • 分块反对角阵的逆矩阵：每个元素取逆矩阵，整个取转置

打洞原理：任意一个矩阵经过一系列初等行变换总能变成阶梯形矩阵

• A可逆——左乘——A干掉C(C处为O) $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|} = \left|\begin{array}{cc} E_m&O\\ -CA^{-1}&E_n \end{array}\right| \left|\begin{array}{ll} A&B\\ C&D \end{array}\right| = \left|\begin{array}{cc} A&B\\ O&D-CA^{-1}B \end{array}\right|$$
• A可逆——右乘——A干掉B(B处为O) $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}={\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}\left|\begin{array}{cc} {E}_{m}&{-A^{-1}B}\\ O&{E}_{n} \end{array}\right|=\left|\begin{array}{cc} A&{O}\\ C&{D-CA^{-1}B} \end{array}\right|$$
• D可逆——左乘——D干掉B $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} {E}_{m}&{-BD^{-1}}\\ O&{E}_{n} \end{array}\right|{\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|} =\left|\begin{array}{cc} {A-BD^{-1}C}&O\\ C&D \end{array}\right|$$
• D可逆——右乘——D干掉C $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}={\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}\left|\begin{array}{cc} {E}_{m}&{O}\\ {-D^{-1}C}&{E}_{n} \end{array}\right|=\left|\begin{array}{cc} {A-BD^{-1}C}&B\\ O&D \end{array}\right|$$
• B可逆——左乘——B干掉D $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} E_m&O\\ -DB^{-1}&E_n \end{array}\right|{\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|} =\left|\begin{array}{cc} A&B\\ C-DB^{-1}A&O \end{array}\right|$$
• B可逆——右乘——B干掉A $$\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|=\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|\left|\begin{array}{cc} E_m&O\\ -B^{-1}A&E_n \end{array}\right|=\left|\begin{array}{cc}O&B\\ C-DB^{-1}A&D \end{array}\right|$$
• C可逆——左乘——C干掉A $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} E_m&-AC^{-1}\\O&E_n \end{array}\right|{\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|} =\left|\begin{array}{cc} O&B-AC^{-1}D\\ C&D \end{array}\right|$$
• C可逆——右乘——C干掉D $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}={\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}\left|\begin{array}{cc} E_m&-C^{-1}D\\ O&E_n \end{array}\right|=\left|\begin{array}{cc}A&B-AC^{-1}D\\ C&O \end{array}\right|$$
• A可逆——既左乘又右乘 $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} {E}_{m}&{O}\\ {-CA^{-1}}&{E}_{n} \end{array}\right|{\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}\left|\begin{array}{cc} {E}_{m}&{-A^{-1}B}\\ O&{E}_{n} \end{array}\right|=\left|\begin{array}{cc} A&{O}\\ {O}&{D-CA^{-1}B} \end{array}\right|$$
• D可逆——既左乘又右乘 $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} {E}_{m}&{-BD^{-1}}\\ O&{E}_{n} \end{array}\right|{\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}\left|\begin{array}{cc} {E}_{m}&{O}\\ {-D^{-1}C}&{E}_{n} \end{array}\right|=\left|\begin{array}{cc} {A-BD^{-1}C}&O\\ {O}&D \end{array}\right|$$
• B可逆——既左乘又右乘 $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} E_m&O\\ -DB^{-1}&E_n \end{array}\right|\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|\left|\begin{array}{cc} E_m&O\\ -B^{-1}A&E_n \end{array}\right|=\left|\begin{array}{cc} O&B\\ C-DB^{-1}A&O \end{array}\right|$$
• C可逆——既左乘又右乘 $${\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|}=\left|\begin{array}{cc} E_m&-AC^{-1}\\O&E_n \end{array}\right|\left|\begin{array}{ll} A&B\\ C&D \end{array}\right|\left|\begin{array}{cc} E_m&-C^{-1}D\\ O&E_n \end{array}\right|=\left|\begin{array}{cc} O&B-AC^{-1}D\\ C&O \end{array}\right|$$

初等行(列)变换

• 定义：下列三种操作分别称为第一类，第二类和第三类初等行(列)变换
  • 交换某两行(列)的位置
  • 用一非零数乘以某一行(列)
  • 将某一行(列)的k倍加到另一行(列)上去

标准形矩阵

• 定义：如果一个矩阵的左上角为单位矩阵，其它位置的元素都为零，则称其为
  (相抵)标准形矩阵
• 任何矩阵都可以经过单纯的初等行变换化为阶梯形矩阵；
• 任何矩阵都可以经过单纯的初等行变换化为Hermite标准型；
• 任何矩阵都可以经过初等变换化为标准形矩阵

子式和子矩阵

• 定义：在矩阵$A= (a_{ij})_{m×n}$中，任取k行k列$(1\le k \le min\{m,n\})$，
  位于这些行列交叉点处的$k^2$个元素按它们在矩阵A中的相对位置构成了一个k阶行列式，称为A的一个k阶子式
• 定义：在矩阵$A=(a_{ij})_{m×n}$中，任取k行l列$(1\le k,l \le min\{m,n\})$，
  位于这些行列交叉点处的元素按它们在矩阵A中的相对位置构成了一个$k×l$ 矩阵,称为A的一个子矩阵

矩阵的秩

• 定义：若在矩阵$A= (a_{ij})_{m×n}$中，存在A的一个r阶子式不为零，但A中任意r＋1阶子式(如果存在的话)都为零，则称r为A的秩，记为r(A)或rank(A)
  • 即矩阵的秩等于它的非零子式的最高阶数
  • 规定O矩阵的秩为0
• 秩的简单性质
  • 若$r(A)= m(n)$，则分别称A是行(列)满秩矩阵
  • 若$r(A) = m = n$，则称A是满秩矩阵
  • A是满秩矩阵$\Leftrightarrow$A是可逆矩阵
  • 若矩阵有r阶子式不为零，则$r(A) \ge r$
  • 若矩阵的所有r阶子式都为零，则$r(A) <r$
  • 对$A$的任意子矩阵$A_1$，有$r(A_1)\le r(A)$
  • $r(A^T)=r(A)$
  • 阶梯型矩阵的秩等于非零行数，标准形矩阵的秩等于其单位阵的阶数
  • 初等变换不改变矩阵的秩
  • $\mathrm{r}\left(A_{m \times n}\right) \leq \min \{m, n\}$
  • $\mathrm{r}\left(\left[\begin{array}{cc}A & O \\O & B\end{array}\right]\right)=\mathrm{r}(A)+\mathrm{r}(B)$
  • $\mathrm{r}\left(\left[\begin{array}{cc}A & O \\C & B\end{array}\right]\right)\ge\mathrm{r}(A)+\mathrm{r}(B)$
  • $\mathrm{r}(A)+\mathrm{r}(B)-n \le \mathrm{r}(A B) \le \min \{\mathrm{r}(A), \mathrm{r}(B)\}$
  • $\max\{\mathrm{r}(A+B),\mathrm{r}(A-B)\}\le \mathrm{r}(A)+\mathrm{r}(B)\le \mathrm{r}(AB)+n$
  • 伴随矩阵的秩：设A是n阶方阵，$A^{*}$是A的伴随矩阵，则 $$r\left(A^{*}\right)=\left\{\begin{array}{ll} n, & r(A)=n \\ 1, & r(A)=n-1 \\ 0, & r(A)<n-1 \end{array}\right.$$

初等矩阵

• 定义：单位矩阵经过一次初等变换得到的矩阵称为初等矩阵
• 定理：用初等矩阵左(右)乘A的效果等同于对A做初等行(列)变换
• 推论：初等矩阵都是可逆矩阵，且其逆为同类型初等矩阵
• 定理：对任何$m \times n$矩阵$A$ , 存在$m$阶初等矩阵$R_{1}, R_{2}, \cdots, R_{s}$，使得$R_{1} R_{2} \cdots R_{s} A$为阶梯型矩阵(Hermite标准形矩阵)，存在$n$阶初等矩阵$C_{1}, C_{2}, \cdots, C_{t}$使得 $$R_{1} R_{2} \cdots R_{s} A C_{1} C_{2} \cdots C_{t}=\left(\begin{array}{cc} E_{r} & O \\ O & O \end{array}\right)$$ 其中$r=\mathrm{r}(A)$
• 初等矩阵的行列式
  • 交换两行后：-1
  • 某一元素是k：k
  • 某一个非对角线元素是k：1
• 初等矩阵的逆
  • 交换两行后：逆矩阵是本身
  • 某一元素是k：改成1/k
  • 某一个非对角线元素是k：改成-k
• 对任何$m \times n$矩阵$A$，存在$m$阶可逆矩阵$P$及$n$阶可逆矩阵$Q$使得 $$P A Q=\left(\begin{array}{cc} E_{r} & O \\ O & O \end{array}\right)$$ 其中$r=r(A)$
  另外有：$r(PAQ)=r(PA)=r(AQ)= r(A)$
• 推论：A可逆$\Leftrightarrow$A的标准形为单位矩阵
• 推论：A可逆$\Leftrightarrow$$A=P_{1} P_{2} \cdots P_{k}$，其中$P_i$为初等矩阵
• 推论：任何一个可逆矩阵可以用初等行变换化为单位矩阵

易错分析：满秩矩阵

• （×）满秩矩阵可分为行满秩矩阵和列满秩矩阵
• （√）满秩矩阵就是可逆矩阵（方阵）

满秩分解：

对 $m \times n$ 阶矩阵$A$,$\mathrm{r}(A)=r$，则存在$m \times r$矩阵$B$与$r \times n$矩阵$C$使得 $A=BC$，且$r(B)=\mathrm{r}(C)=r$（满秩分解不唯一）

初等变换法求逆矩阵：略

• 如果A不可逆，使用这一过程会发生什么情况？无法将左边化成单位矩阵

等价或相抵

• 定义：如果矩阵A经过有限次初等变换后变为矩阵B，则称二者等价或相抵.
• 定理矩阵A与B相抵的充要条件是存在可逆矩阵P，Q使得$PAQ=B$
• 矩阵的相抵关系满足以下性质：
  • 自反性: $EAE=A$
  • 对称性: $PAQ=B \Rightarrow P^{-1} B Q^{-1}=A$
  • 传递性: $$\left.\begin{array}{l} P_{1} A Q_{1}=B \\ P_{2} B Q_{2}=C \end{array}\right\} \Rightarrow\left(P_{2} P_{1}\right) A\left(Q_{1} Q_{2}\right)=C$$

矩阵之间的关系

• $$\begin{align} |A|\ne 0 \Leftrightarrow & A是非奇异矩阵 \\ \Leftrightarrow & A是可逆矩阵 \\ \Leftrightarrow & A是满秩矩阵 \\ \end{align}$$

• 非方阵既不是奇异矩阵也不是非奇异矩阵

AB与BA的爱恨情仇

• 若$A$为$m×n$矩阵，$B$为$n×m$矩阵，则：
  • $A(I_n-BA)=(I_m-AB)A$
  • 若$I_m-AB$可逆，则$(I_n-BA)^{-1}=I_n+B(I_m-AB)^{-1}A$
  • $|I_m-AB|=|I_n-BA|$
  • 若$m=n$，$AB=I$，则$BA=I$
  • 若$m>n$，不存在$AB=I_m$（用秩来证）
  • 若$m<n$，$AB=I_m$，不一定有$BA=I_n$（比如$A=[1,0],B=[1,0]^\mathrm{T}$）
  • $tr(AB)=tr(BA)$
  • $|\lambda I_m-AB|=\lambda^{m-n}|\lambda I_n-BA|$
  • 若$|BA|\ne 0$，则$AB$可对角化的充要条件是$BA$可对角化
  • $r(I_m-AB)+n=r(I_n-BA)+m$

用函数解线代题

回归源头：矩阵与方程组解的联系

第三章 n维向量与线性方程组解的结构

n维向量

• 定义：略
• 实向量、复向量
• 列向量、行向量
• 零向量、负向量
• 如果向量的元素在数域$\mathbb{K}$上，全体$n$维向量记为$\mathbb{K}^n$
• 如果向量的元素在实数域上，全体$n$维向量记为$\mathbb{R}^n$

向量的线性运算

• 加法、数乘的定义：略
• 性质：设 $\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}$ 为任意$n$维向量, $k, l$ 取自实数域 $\mathbb{R}$ , 则
  (1) $\boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{\beta}+\boldsymbol{\alpha}$ , 加法交换律;
  (2) $(\boldsymbol{\alpha}+\boldsymbol{\beta})+\boldsymbol{\gamma}=\boldsymbol{\alpha}+(\boldsymbol{\beta}+\boldsymbol{\gamma})$ , 加法结合律;
  (3) 零元存在: 对任意 $\boldsymbol{\alpha}$ , 有 $\mathbf{0}+\boldsymbol{\alpha}=\boldsymbol{\alpha}+\mathbf{0}=\boldsymbol{\alpha}$ ;
  (4) 负向量存在: 对任意 $\boldsymbol{\alpha}$ , 有 $\boldsymbol{\alpha}+(-\boldsymbol{\alpha})=\mathbf{0}$ ;
  (5) 对数 $1$, 有 $1 \cdot \boldsymbol{\alpha}=\boldsymbol{\alpha}$ ;
  (6) $(k \cdot l) \boldsymbol{\alpha}=k(l \boldsymbol{\alpha})$ ;
  (7) $(k+l) \boldsymbol{\alpha}=k \boldsymbol{\alpha}+l \boldsymbol{\alpha}$ ;
  (8) $k(\boldsymbol{\alpha}+\boldsymbol{\beta})=k \boldsymbol{\alpha}+k \boldsymbol{\beta}$

线性方程组的向量表示

• 定义：对于$n$维向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m},\boldsymbol{\beta}$，如果存在一组数$k_1,k_2,\cdots,k_m$,使得$\boldsymbol{\beta}=k_1\boldsymbol{\alpha}_{1}+k_2\boldsymbol{\alpha}_{2}+\cdots+k_m\boldsymbol{\alpha}_{m}$,称$\boldsymbol{\beta}$是$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$的一个线性组合，或称向量$\boldsymbol{\beta}$能由$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$线性表示（表出），$k_1,k_2,\cdots,k_m$为组合系数或表示系数。
• 零向量可以由任意向量线性表出

线性表示与线性方程组的关系

• 定理：向量$\boldsymbol{\beta}$能由向量$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$线性表出$\Leftrightarrow$线性方程组$x_1\boldsymbol{\alpha}_{1}+x_2\boldsymbol{\alpha}_{2}+\cdots+x_m\boldsymbol{\alpha}_{m}=\boldsymbol{\beta}$有解或$(\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m})X=b$有解
• 定理：$n$维向量$\boldsymbol{\beta}$可由向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$线性表示的充分必要条件为 $$r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}})$$ 其中 $\boldsymbol{A}=(\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m})$，$\widetilde{\boldsymbol{A}}=(\boldsymbol{A}, \boldsymbol{\beta}) $. 进而：
  • $\boldsymbol{\beta}$ 可由 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots , \boldsymbol{\alpha}_{m}$ 线性表示且表示系数唯一的充分必要条件是 $r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}})=m$ ；
  • $\boldsymbol{\beta}$ 可由 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性表示且表示系数不唯一的充分必要条件是 $r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}})<m $；
  • $\boldsymbol{\beta}$ 不能由 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性表示的充分必要条件是 $r(\boldsymbol{A}) \neq r(\tilde{\boldsymbol{A}})$

向量组之间的关系

• 若向量组(I)$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$中的任意向量都能由向量组(II)$\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{s}$线性表示，则称向量组(I)能由向量组(II)线性表示；同时向量组(II)也能由向量组(I)线性表示，即这两个向量组互相线性表示，则称向量组(I)$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$与向量组(II)$\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{s}$等价。
• 命题：向量组$\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{t}$可由向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$线性表示的充分必要条件为 $$r(\boldsymbol{A})=r(\boldsymbol{B}),$$ 其中矩阵$\boldsymbol{A}$是以向量$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$为列构造的矩阵, 矩阵$\boldsymbol{B}$是以向量$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}, \boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{t}$为列构造的矩阵.
• 矩阵$A,B$行向量组等价的充要条件是$\mathrm{r}(A)=\mathrm{r}(B)=\mathrm{r}\left(\begin{array}{c}\boldsymbol{A}\\ \boldsymbol{B}\end{array}\right)$
• 矩阵$A,B$列向量组等价的充要条件是$\mathrm{r}(A)=\mathrm{r}(B)=\mathrm{r}\left(\boldsymbol{A},\boldsymbol{B}\right)$
• 向量组等价的性质
  • 反身性
  • 对称性
  • 传递性

线性相关与线性无关

• 定义：对向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$若存在一组不全为零的数$k_1,k_2,\cdots,k_m$使得$k_1\boldsymbol{\alpha}_{1}+k_2\boldsymbol{\alpha}_{2}+\cdots+k_m\boldsymbol{\alpha}_{m}=0$，则称此向量组线性相关，否则称为线性无关。
• 等价定义：若向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$中存在一个向量能由其它向量线性表出，则称此向量组线性相关，否则称为线性无关。
• 推论：
  • 单个向量$\boldsymbol{\alpha}$构成的向量组线性相关的充要条件是该向量$\boldsymbol{\alpha}$为零向量。
  • 向量组含有零向量必线性相关
• 定理：n维向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{m}$线性相关（无关）的充要条件是方程组$x_1\boldsymbol{\alpha}_{1}+x_2\boldsymbol{\alpha}_{2}+\cdots+x_m\boldsymbol{\alpha}_{m}=\boldsymbol{0}$有非零解（唯一零解）

• 推论1：令

  $$\boldsymbol{\alpha}_{1}=\left(\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{n 1} \end{array}\right), \boldsymbol{\alpha}_{2}=\left(\begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{n 2} \end{array}\right), \cdots, \boldsymbol{\alpha}_{m}=\left(\begin{array}{c} a_{1 m} \\ a_{2 m} \\ \vdots \\ a_{n m} \end{array}\right)$$

  则向量$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$线性相关的充分必要条件是 $r(\boldsymbol{A})<m$ ; 向量 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性无关的充分必要条件是 $r(\boldsymbol{A})=m$, 其中

  $$\boldsymbol{A}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}\right)$$

• 推论2：$n$个$n$维向量 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}$线性相关的充分必要条件是

  $$|\boldsymbol{A}|=0$$

  $n$个$n$维向量 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}$线性无关的充分必要条件是

  $$|\boldsymbol{A}|\ne 0$$

  其中$\boldsymbol{A}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right)$

• 对于$\mathbb{R}^n$中任意$m$个向量，当$m>n$时必线性相关。

整体与部分的线性相关性

• 定理1：若向量组中有部分向量线性相关，则该向量组线性相关；反之，若向量组线性无关，则部分向量构成的向量组也线性无关。（部分相关，则整体相关；整体无关，则部分无关）
• 定理2：若向量组线性相关，则其截短向量组（向量组各向量截取一些对应位置的元素）也线性相关；反之，若向量组线性无关，则其接长向量组（向量组各向量增加一些对应位置的元素）也线性无关。（原向量组相关，截短也相关；原向量组无关，则接长无关）
• 定理3：向量组 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性相关, $\boldsymbol{\alpha}_{1}$ 不能由 $\boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性表示, 则 $\boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性相关;

线性相关性的传递

• 设向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$线性无关, 向量组$\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots , \boldsymbol{\beta}_{s}$可由$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$线性表示, 即$\left(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{s}\right)$= $\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}\right) \boldsymbol{A}_{m \times s}$. 则$\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{s}$线性相关 (线性无关) 的充分必要条件为$r(\boldsymbol{A})<s$（$r(\boldsymbol{A})=s$）

线性组合与线性相关的关系

• 定理1：若向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}(m\ge 2)$线性相关，至少存在一个向量可由其余$m-1$个向量线性表出。

• 定理2：若向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$线性无关,而向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m},\boldsymbol{\beta}$线性相关，则$\boldsymbol{\beta}$可由$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$线性表出，且表示系数唯一。

极大线性无关组

• 定义：设向量组 $I : \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}, \cdots$(向量个数可有限也可无限)，若存在它的部分向量组 $II: \boldsymbol{\alpha}_{i_{1}}, \boldsymbol{\alpha}_{i_{2}}, \cdots, \boldsymbol{\alpha}_{i_{r}}$，满足:
  (1) $\boldsymbol{\alpha}_{i_{1}}, \boldsymbol{\alpha}_{i_{2}}, \cdots, \boldsymbol{\alpha}_{i_{r}}$线性无关；
  (2) 向量组 $I$ 中的每一个向量都可由向量组 $II$ 线性表示,
  则称向量组 $II:\alpha_{i_{1}}, \alpha_{i_{2}}, \cdots, \alpha_{i_{r}}$是向量组$I$的一个极大线性无关组，简称极大无关组。
• 一般地，向量组的极大无关组不唯一
• 事实上，一个向量组的极大无关组唯一当且仅当这个向量组去掉(可能的)零向量以后本身就是个无关向量组
• 定义全零向量组的极大无关组为空集
• 一个向量组若存在极大线性无关组，则这个向量组与其极大无关组等价
• 若向量组的极大无关组不唯一，则其任意两个极大无关组等价

向量组的替换定理

• 设两个向量组 $(I)\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{r}$，与$(I)\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots , \boldsymbol{\beta}_{s}$，且(I)能由(II)线性表出，
  (1)当 $r>s$ , 则 $(I)$ 线性相关
  (2)当 $(I)$ 线性无关时, 必有 $ r \leq s $
• 推论：
  • 两个等价的线性无关的向量组所含向量个数相等
  • 向量组的两个极大无关组所含向量的个数相同

向量组的秩

• 定义：向量组的极大线性无关组所含向量的个数称为向量组的秩，记作$\mathrm{r}(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m})$
• 规定：由零向量组成的向量组的秩为0
• 向量组 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性无关的充要条件是 $\mathrm{r}(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m})=m$
• 向量组 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$ 线性相关的充要条件是 $\mathrm{r}(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m})<m$
• 等价的向量组必有相同的秩
• 若向量组的秩$\mathrm{r}>0$，则向量组中任意$\mathrm{r}$个线性无关向量都是它的一个极大线性无关组
• 若向量组$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s}$可由向量组$\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{t}$线性表示，则 $$\mathrm{r}(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s})\le \mathrm{r}(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{t})$$

向量组的秩与矩阵的秩

• 定理：$\mathrm{r}(A) =\mathrm{r}(A的行向量组）=\mathrm{r}(A的列向量组)$
• 矩阵的行变换不改变列的线性相关关系
• 矩阵的列变换不改变列的线性相关关系
• 矩阵的列向量组的秩又称为矩阵的列秩
• 矩阵的行向量组的秩又称为矩阵的行秩
• 行秩=列秩=秩. 所以我们可以统称为秩
• $\mathrm{r}(A+B)\le \mathrm{r}(A)+\mathrm{r}(B)$
• $max\{\mathrm{r}(A),\mathrm{r}(B)\}\le \mathrm{r}(A,B)\le \mathrm{r}(A)+\mathrm{r}(B)$
• $\mathrm{r}(AB)\le min\{\mathrm{r}(A),\mathrm{r}(B)\}$

基础解系

• 引理：设有齐次线性方程组$\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0}$，若$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{s}$是方程组的$s$个解向量，则它们的线性组合$\sum_{i=1}^{s} k_{i} \boldsymbol{\eta}_{i}$仍是齐次线性方程组$\boldsymbol{A x}=\mathbf{0}$的解向量，其中$k_{1} , k_{2}, \cdots, k_{s}$为任意常数
• 定义：设$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{p}$是齐次线性方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$的一组解向量，如果:
  (1)$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{p}$线性无关；
  (2)齐次线性方程组$\boldsymbol{A x}=\mathbf{0}$的任意一个解向量都可由$\boldsymbol{\eta}_{1} , \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{p}$线性表示，
  则称$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{p}$是齐次线性方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$ 的一个基础解系
• 定理：设$A$是$m \times n$矩阵，若$r(A)=r<n$，则齐次线性方程组$\boldsymbol{A}\boldsymbol{x}=\mathbf{0}$存在一个由$n-r$个线性无关的解向量$\boldsymbol{\eta}_{1},\boldsymbol{\eta}_{2},\cdots,\boldsymbol{\eta}_{n-r}$构成的基础解系，它们的线性组合 $$\tilde{\boldsymbol{\eta}}=k_{1} \boldsymbol{\eta}_{1}+k_{2} \boldsymbol{\eta}_{2}+\cdots+k_{n-r} \boldsymbol{\eta}_{n-r}$$ （其中$k_{1}, k_{2}, \cdots, k_{n-r}$为任意常数）给出了齐次线性方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$的所有解。形如上式的解被称为方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$的通解
• 齐次线性方程组的基础解系不唯一
• 基础解系包含的解向量的个数唯一($n-r(A)$)
• 基础解系之间等价
• 设$r(A)= r$, 则齐次线性方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$的任意$n-r$个线性无关的解向量都可以作为它的基础解系

方程同解相关

• 方程$\boldsymbol{A}\boldsymbol{X}=\mathbf{0}$与$\boldsymbol{B}\boldsymbol{X}=\mathbf{0}$同解的充分必要条件是$\boldsymbol{A},\boldsymbol{B}$的行向量组等价，即$\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{B})=\mathrm{r}\left(\begin{array}{c}\boldsymbol{A}\\ \boldsymbol{B}\end{array}\right)$
• 若$\mathrm{r}(\boldsymbol{A}^k)=\mathrm{r}(\boldsymbol{A}^{k+1})$，则存在非异阵$\boldsymbol{P}$，使得$\boldsymbol{P}\boldsymbol{A}^k=\boldsymbol{A}^{k+1}$
• 对$n$阶方阵$\boldsymbol{A}$，有$\mathrm{r}(\boldsymbol{A}^n)=\mathrm{r}(\boldsymbol{A}^{n+1})$

求齐次线性方程组的通解

(1) 用初等行变换将齐次线性方程组的系数矩阵化为行最简形

$$A \stackrel{r}{\longrightarrow} R_{A}=\left(\begin{array}{cc} E_{r} & A_{0} \\ 0 & 0 \end{array}\right)$$

(2) 根据规范阶梯形（Hermite形）写出其基础解系

$$\left(\begin{array}{c} -A_{0} \\ E_{n-r} \end{array}\right) \text { 的 } n-r \text { 个列向量为一个基础解系 }$$

(3)基础解系的线性组合即为通解

• $\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0}$有无数组非零解的充分必要条件是 $\mathrm{r}(\boldsymbol{A})<n$ ；

• $\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0}$无非零解的充分必要条件是 $\mathrm{r}(\boldsymbol{A})=n$ ；

• 用齐次方程组解的性质证明下列结论：
  设$A,B$分别为$m×n$和$n×s$矩阵，且$AB＝0$，则$R(A)＋R(B)\le n$

  非齐次线性方程组解的结构

• 定义：对于非齐次线性方程组$\boldsymbol{A_{m\times n}x}=\boldsymbol{b}$，称$\boldsymbol{A x}=\mathbf{0}$为$\boldsymbol{A x}=\mathbf{b}$对应的齐次线性方程组(或导出组)
• 定理1：若$\boldsymbol{\gamma}_{1}, \boldsymbol{\gamma}_{2}$是$\boldsymbol{A x}=\boldsymbol{\beta}$的任意两个解向量, 则$\boldsymbol{\gamma}_{1}-\boldsymbol{\gamma}_{2}$是对应的齐次线性方程组$\boldsymbol{A x}=\mathbf{0}$的解向量.
• 定理2：设$\boldsymbol{\gamma}_{0}$是$\boldsymbol{A x}=\boldsymbol{\beta}$的一个解向量,$\boldsymbol{\eta}$是对应的齐次线性方程组$\boldsymbol{A x}=\mathbf{0}$的任一解向量, 则$\boldsymbol{\gamma}_{0}+\boldsymbol{\eta}$仍是$\boldsymbol{A x}=\boldsymbol{\beta}$的一个解向量.
• 定理3：$\boldsymbol{A x}=\boldsymbol{\beta}$的任一解向量$\boldsymbol{\gamma}$都可表示成$\boldsymbol{\gamma}=\boldsymbol{\gamma}_{0}+\boldsymbol{\eta}$，其中$\boldsymbol{\gamma}_{0}$是$\boldsymbol{A x}=\boldsymbol{\beta}$的某个解向量，$\boldsymbol{\eta}$是对应的齐次线性方程组的某个解向量.
• 定理4：若非齐次线性方程组$\boldsymbol{A x}=\boldsymbol{\beta}$满足$\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{\beta})=r$，$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n-r}$是对应的齐次线性方程组$\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$的基础解系,$\gamma_{0}$是$\boldsymbol{A x}=\boldsymbol{\beta}$的某个解（称为特解）, 则 $$\boldsymbol{x}=\boldsymbol{\gamma}_{0}+k_{1} \boldsymbol{\eta}_{1}+k_{2} \boldsymbol{\eta}_{2}+\cdots+k_{n-r} \boldsymbol{\eta}_{n-r}$$ （其中$k_{1}, k_{2}, \cdots, k_{n-r}$是任意常数）给出了$\boldsymbol{A x}=\boldsymbol{\beta}$的所有解，称为通解

求非齐次线性方程组的通解的步骤

(1) 用初等行变换将增广矩阵化为行最简形,

$$\widetilde{A} \stackrel{r}{\rightarrow}\left(\begin{array}{ccc} E_{r} & A_{0} & b_{0} \\ 0 & 0 & 0 \end{array}\right)$$

(2) 根据规范阶梯形（Hermite型）写出对应齐次的基础解系和非齐次特解，

$$\left(\begin{array}{c}-A_{0} \\ E_{n-r}\end{array}\right) \text{的} n-r \text{个列向量为一个基础解系，}$$ $$\left(\begin{array}{c}b_{0} \\0_{n-r}\end{array}\right) \text { 为非齐次的一个特解 }$$

(3)齐次通解加非齐次特解即为非齐次通解。

• $\boldsymbol{A}_{m \times n} \boldsymbol{x}=\boldsymbol{b}$有无数组解的充分必要条件是 $\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A},\boldsymbol{b})<n$ ；
• $\boldsymbol{A}_{m \times n} \boldsymbol{x}=\boldsymbol{b}$只有一组解的充分必要条件是 $\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A},\boldsymbol{b})=n$ ；
• $\boldsymbol{A}_{m \times n} \boldsymbol{x}=\boldsymbol{b}$无解的充分必要条件是 $\mathrm{r}(\boldsymbol{A})\ne\mathrm{r}(\boldsymbol{A},\boldsymbol{b})$ ；

第四章 线性空间与线性变换

线性空间的定义

　　设$V$是一个非空集合，$F$是数域。在$V$的元素之间定义加法运算，记作“+”，即对任意两个元素$\boldsymbol{\alpha}, \boldsymbol{\beta} \in V$，有唯一的一个元素$\boldsymbol{\delta} \in V$与之对应，称$\boldsymbol{\delta}$为$\boldsymbol{\alpha}$和$\boldsymbol{\beta}$的和，记作$\boldsymbol{\delta}=\boldsymbol{\alpha}+\boldsymbol{\beta}$. 并且加法运算“+”满足：
(1) 交换律：$\boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{\beta}+\boldsymbol{\alpha}$
(2) 结合律：$(\boldsymbol{\alpha}+\boldsymbol{\beta})+\boldsymbol{\gamma}=\boldsymbol{\alpha}+(\boldsymbol{\beta}+\boldsymbol{\gamma})$
(3) 零元存在性：$V$中存在一个零元$\mathbf{0}$。对$\forall \boldsymbol{\alpha} \in V$，有$\boldsymbol{\alpha}+\mathbf{0}=\boldsymbol{\alpha}$
(4) 负元存在性：对任意$\boldsymbol{\alpha} \in V$，都存在$\boldsymbol{\beta} \in V$，称$\boldsymbol{\beta}$为$\boldsymbol{\alpha}$的负元，使得$\boldsymbol{\alpha}+\boldsymbol{\beta}=\mathbf{0}$
　　在数域$F$和集合$V$之间还定义一个运算，称为纯量乘法，即对$\forall \boldsymbol{\alpha} \in V$和$k \in F$，有唯一的元素$\boldsymbol{\eta} \in V$与之对应，称为$k$与$\boldsymbol{\alpha}$的乘积，记为$\boldsymbol{\eta}=k \boldsymbol{\alpha}$，使对任意$k, l \in F, \boldsymbol{\alpha}$,$\boldsymbol{\beta} \in V$，都有:
(5)$1 \boldsymbol{\alpha}=\boldsymbol{\alpha}$
(6)$k(l \boldsymbol{\alpha})=l(k \boldsymbol{\alpha})=(k l) \boldsymbol{\alpha}$
(7)$(k+l) \boldsymbol{\alpha}=k \boldsymbol{\alpha}+l \boldsymbol{\alpha}$
(8)$k(\boldsymbol{\alpha}+\boldsymbol{\beta})=k \boldsymbol{\alpha}+k \boldsymbol{\beta}$
　　则称集合$V$关于向量加法与纯量乘法组成数域$F$上的一个线性空间，或称$V$为$F$上的一个线性空间。
　　特别地，当$F$为实数域时，称$V$为实线性空间.

• 凡满足以上八条规律的加法及数乘运算，称为线性运算
• 判别线性空间的方法：一个集合，对于定义的加法和数乘运算不封闭，或者运算不满足八条性质的任一条，则此集合就不能构成线性空间
• 线性空间的元素统称为“向量”，但它可以是通常的向量，也可以是矩阵、多项式、函数等

常见的线性空间

$F^n$,$F^{m \times n}$,$C[a,b]$,$\mathbb{R}[x]$,$D^{(n)}[a,b]$

线性空间的简单性质

设$V$是数域$F$上的线性空间，则
(1) 零元唯一，记作$\boldsymbol{0}$
(2) $V$中元素$\boldsymbol{\alpha}$的负元唯一，记为$-\boldsymbol{\alpha}$
(3) $\forall \boldsymbol{\alpha} \in V$，有$0 \boldsymbol{\alpha}=\mathbf{0}$,$(-1)\boldsymbol{\alpha}=-\boldsymbol{\alpha}$
(4) $\forall k \in F$，有$k \boldsymbol{0}=\mathbf{0}$
(5) 若 $k \boldsymbol{\alpha}=\boldsymbol{0}$，则有 $k=0$ 或 $\boldsymbol{\alpha}=\mathbf{0}$

线性空间的子空间

设V是数域F上的一个线性空间，W是V的一个非空子集，如果V对于W中所定义的加法和数乘两种运算也构成一个数域F上的线性空间，则称W为V的子空间

• $n$阶实对称矩阵的集合是$R^{n\times n}$的子空间
• $n$阶实反对称矩阵的集合是$R^{n\times n}$的子空间
• 以实矩阵$A_{m \times n}$为系数矩阵的齐次线性方程组$\boldsymbol{A x}=\mathbf{0}$的解向量的全体所组成的集合构成$R^n$的子空间，称之为齐次解空间
• 以实矩阵$A_{m \times n}$为系数矩阵的非齐次线性方程组$\boldsymbol{A x}=\boldsymbol{b}$的解向量的全体所组成的集合不构成$R^n$的子空间
• 线性子空间的交仍为线性子空间
• 线性子空间的并不一定是线性子空间

向量的线性相关性定义

略

维数与基的定义

在线性空间$V$中，如果存在$n$个元素$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}$满足：
(1) $\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}$线性无关
(2) $V$中任一元素$\boldsymbol{\alpha}$总可由$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}$线性表示
那么$\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}$称为线性空间$V$的一个基，$n$称为线性空间的维数，记$\mathrm{dim} V = n$

• 维数为$n$的线性空间称为$n$维线性空间，记作$V_n$
• W={三阶实对称矩阵}，dim W=6
• 零向量构成的线性空间$\{\mathbf{0}\}$没有基，不妨规定$\mathrm{dim}\{\mathbf{0}\} =0$
• 线性空间的基不唯一
• 基所含的元素的个数唯一（维数）
• 不同的基之间是等价的
• $n$维线性空间与$0$维线性空间统称为有限维线性空间，或有限生成的线性空间。如果$V$不是有限生成的，或者说，如果$V$中含有无限多个线性无关的向量，称$V$为无限维线性空间。

坐标的定义

设$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}$是$n$维线性空间$V$的一组基，$\boldsymbol{\gamma} \in V$，且

$$\boldsymbol{\gamma}=x_{1} \boldsymbol{\alpha}_{1}+x_{2} \boldsymbol{\alpha}_{2}+\cdots+x_{n} \boldsymbol{\alpha}_{n}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right) \boldsymbol{x}$$

其中

$$\boldsymbol{x}=\left(\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right)$$

称向量$\boldsymbol{x}$为$\boldsymbol{\gamma}$在基$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}$下的坐标

同构映射的定义

设$V$和$V^{\prime}$是数域$F$上的两个线性空间，如果存在$V$到$V^{\prime}$上的一个满足下述条件的一一对应$\sigma:$
(1) $\sigma(\boldsymbol{\alpha}+\boldsymbol{\beta})=\sigma(\boldsymbol{\alpha})+\sigma(\boldsymbol{\beta}), \forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V$
(2) $\sigma(k \boldsymbol{\alpha})=k \sigma(\boldsymbol{\alpha}), \forall \boldsymbol{\alpha} \in V, \forall k \in F$
则称$\sigma$为线性空间$V$到$V^{\prime}$的一个同构映射，也称线性空间$V$与$V^{\prime}$同构，记作$V\cong V^{\prime}$

• 数域$F$上的任何$n$维线性空间$V$都与$F^n$同构
• 同构的线性空间维数相同

基变换公式

设$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$和$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}$是$n$维线性空间$V$中的两组基，且

$$\left(\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}\right)=\left(\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}\right) \boldsymbol{C}$$

则称矩阵$\boldsymbol{C}=\left(c_{i j}\right)_{n \times n}$为由基$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$到基$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}$的过渡矩阵，上式称为基变换公式

• 过渡矩阵$\boldsymbol{C}$是可逆的

坐标变换公式

设$V_n$中的元素$\boldsymbol{\alpha}$在基$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$下的坐标为$\boldsymbol{x}=\left(x_{1}, x_{2}, \cdots, x_{n}\right)^{T}$，在基$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}$下的坐标为$\boldsymbol{x’}=\left(x_{1}^{\prime}, x_{2}^{\prime}, \cdots, x_{n}^{\prime}\right)^{T}$
若两个基满足关系式

$$\left(\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}\right)=\left(\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}\right) \boldsymbol{C}$$

则有坐标变换公式

$$\boldsymbol{x'}=\boldsymbol{C}^{-1}\boldsymbol{x}$$

或者

$$\boldsymbol{x}=\boldsymbol{C}\boldsymbol{x'}$$

欧氏空间的定义

设$V$为实数域$\mathbb{R}$上的一个线性空间. 对$V$中的任意一对元素$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$，都有$\mathbb{R}$中唯一的一个实数与之对应，将此实数记作$(\boldsymbol{\alpha}, \boldsymbol{\beta})$，若此对应关系满足以下条件：
(1) 对称性：$(\boldsymbol{\alpha}, \boldsymbol{\beta})=(\boldsymbol{\beta}, \boldsymbol{\alpha})$,$ \forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V$
(2) 线性性：$(k \boldsymbol{\alpha}+l \boldsymbol{\beta}, \boldsymbol{\gamma})=k(\boldsymbol{\alpha}, \gamma)+l(\boldsymbol{\beta}, \gamma)$, $\forall k, l \in \mathbb{R}$ , $\boldsymbol{\alpha}, \boldsymbol{\beta}, \gamma \in V $
(3) 正定性：$(\boldsymbol{\alpha}, \boldsymbol{\alpha}) \geqslant 0$且$(\boldsymbol{\alpha}, \boldsymbol{\alpha})=0$的充分必要条件是 $\alpha=0$
则称$(\boldsymbol{\alpha}, \boldsymbol{\beta})$为向量$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$的内积，定义了内积的实线性空间$V$称之为一个欧几里得空间，简称欧氏空间

常见的内积

• n维普通向量
  对应项乘积之和
• $R^{m\times n}$中
  对应项乘积之和
• 在C[a,b]中
  $(f,g)=\int_a^b f(x)g(x)\mathrm{d}x$

长度的定义

设$V$为欧氏空间，对$V$中任意向量$\boldsymbol{\alpha}$，令

$$|\boldsymbol{\alpha}|=\sqrt{(\boldsymbol{\alpha},\boldsymbol{\alpha})}$$

称$|\boldsymbol{\alpha}|$为向量$|\boldsymbol{\alpha}|$的长度（模），若$|\boldsymbol{\alpha}|=1$，则称$\boldsymbol{\alpha}$为单位向量

欧氏空间的性质

设$V$为欧氏空间，$\boldsymbol{\alpha}, \boldsymbol{\beta} \in V$, $k \in \mathbb{R}$，则

• $|\boldsymbol{\alpha}| \geqslant 0$，且$|\boldsymbol{\alpha}|=0$ 的充分必要条件是$\boldsymbol{\alpha}=\mathbf{0}$
• $|k \boldsymbol{\alpha}|=|k| \cdot|\boldsymbol{\alpha}|$, $\forall k \in K, \boldsymbol{\alpha} \in V$
• (柯西-施瓦茨 (Cauchy-Schwarz) 不等式)$|(\boldsymbol{\alpha}, \boldsymbol{\beta})| \leqslant |\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|$, $\forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V$，当且仅当$\boldsymbol{\alpha}$ 与 $\boldsymbol{\beta} $线性相关时$|(\boldsymbol{\alpha}, \boldsymbol{\beta})|=|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|$
• (三角不等式)$|\boldsymbol{\alpha}+\boldsymbol{\beta}|\le |\boldsymbol{\alpha}|+|\boldsymbol{\beta}|$

夹角与正交的定义

设$V$为欧氏空间，$\alpha, \beta$为$V$中的非零向量. 令

$$\langle\boldsymbol{\alpha}, \boldsymbol{\beta}\rangle=\arccos \frac{(\boldsymbol{\alpha}, \boldsymbol{\beta})}{|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|}$$

则称$\langle\boldsymbol{\alpha}, \boldsymbol{\beta}\rangle$为向量$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$的夹角. 特别地, 当$ (\boldsymbol{\alpha}, \boldsymbol{\beta})=0$时称$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$正交，记作$\boldsymbol{\alpha} \perp \boldsymbol{\beta}$

• 零向量$\mathbf{0}$可看作与$V$中任意向量都正交

正交向量组

设$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_s$ 为欧氏空间$V$中一组非零向量. 若对任意$1 \leqslant i, j \leqslant s$, 当 $i \neq j$ 时都有 $\boldsymbol{\alpha}_{i} \perp \boldsymbol{\alpha}_{j} $，则称向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_s $为一个正交向量组

• 正交向量组一定线性无关，线性无关的向量组不一定正交

距离的定义

设$V$为欧氏空间，对$\boldsymbol{\alpha}, \boldsymbol{\beta} \in V$，令

$$d(\boldsymbol{\alpha}, \boldsymbol{\beta})=|\boldsymbol{\alpha}-\boldsymbol{\beta}|$$

称$d(\boldsymbol{\alpha}, \boldsymbol{\beta})$为向量$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$的距离，即向量$\boldsymbol{\alpha}$与$\boldsymbol{\beta}$的距离等于向量$\boldsymbol{\alpha}-\boldsymbol{\beta}$的长度

标准正交基

设$\varepsilon_{1}, \varepsilon_{2}, \cdots, \varepsilon_{n}$为$n$维欧氏空间$V$的一个正交向量组. 因此是$V$的一组基，称为$V$的一组正交基. 若正交基中每一个向量都是单位向量。则称此正交基为标准正交基.

• 欧氏空间中标准正交基一定是存在的

施密特(Aram-Schmidt)正交化

设$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$是线性无关的向量组$(s \geqslant 2)$
(1) 正交化，令

$$\begin{aligned} \boldsymbol{\beta}_{1}=&\boldsymbol{\alpha}_{1},\\ \boldsymbol{\beta}_{2}=& \boldsymbol{\alpha}_{2}-\frac{\left(\boldsymbol{\alpha}_{2}, \boldsymbol{\beta}_{1}\right)}{\left(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{1}\right)} \boldsymbol{\beta}_{1}, \\ \boldsymbol{\beta}_{3}=& \boldsymbol{\alpha}_{3}-\frac{\left(\boldsymbol{\alpha}_{3}, \boldsymbol{\beta}_{1}\right)}{\left(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{1}\right)} \boldsymbol{\beta}_{1}-\frac{\left(\boldsymbol{\alpha}_{3}, \boldsymbol{\beta}_{2}\right)}{\left(\boldsymbol{\beta}_{2}, \boldsymbol{\beta}_{2}\right)} \boldsymbol{\beta}_{2} \\ \vdots \\ & \\ \boldsymbol{\beta}_{s}=&\boldsymbol{\alpha}_{s}-\frac{\left(\boldsymbol{\alpha}_{s}, \boldsymbol{\beta}_{1}\right)}{\left(\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{1}\right)}\boldsymbol{\beta}_{1}-\cdots-\frac{\left(\boldsymbol{\alpha}_{s}, \boldsymbol{\beta}_{s-1}\right)}{\left(\boldsymbol{\beta}_{s-1}, \boldsymbol{\beta}_{s-1}\right)} \boldsymbol{\beta}_{s-1} . \end{aligned}$$

则$\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{s}$是正交向量组.
(2) 单位化，令

$$\boldsymbol{\eta}_{i}=\frac{1}{\left|\boldsymbol{\beta}_{i}\right|} \boldsymbol{\beta}_{i}(i=1,2, \cdots, s)$$

则$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{s}$为标准正交向量组.

正交矩阵

设$A$为$n$阶实矩阵，若$A$的列（行）向量组是标准正交向量组. 即若记

$$A=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right)$$

$A$的列向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}$满足

$$\left(\boldsymbol{\alpha}_{i}, \boldsymbol{\alpha}_{j}\right)=\left\{\begin{array}{l} 0, i \neq j \\ 1, i=j \end{array} \quad(i, j=1,2, \cdots, n),\right.$$

则称$A$为正交矩阵

• 定理：$n$阶实矩阵$A$为正交矩阵的充分必要条件为$\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}=\boldsymbol{E}$

正交矩阵的性质

• 若$\boldsymbol{A}$为正交矩阵，则$|\boldsymbol{A}|=\pm 1$
• 实矩阵$\boldsymbol{A}$为正交矩阵的充要条件为$\boldsymbol{A}^{-1}=\boldsymbol{A}^{\mathrm{T}}$
• 若矩阵$\boldsymbol{A}$为正交矩阵，则$\boldsymbol{A}^{-1},\boldsymbol{A}^{*},\boldsymbol{A}^k,\boldsymbol{A}^{\mathrm{T}}$也是正交矩阵
• 若$n$阶矩阵$\boldsymbol{A}$和$\boldsymbol{B}$都是正交矩阵，则乘积$\boldsymbol{A B}$也是正交矩阵
• $\boldsymbol{A}$是非零实矩阵，若$\boldsymbol{A}^{\star}=\boldsymbol{A}^{\mathrm{T}}$，则$\boldsymbol{A}$为正交矩阵

线性变换的概念

设$V$是数域$F$上的线性空间，若$\mathscr{A}$是线性空间$V$到自身的一个映射，即对$\forall \alpha \in V$，有唯一的向量$\boldsymbol{\beta} \in V$与$\boldsymbol{\alpha}$对应，则称$\mathscr{A}$为$V$的一个变换。进而，若变换$\mathscr{A}$满足：
(1) $\mathscr{A}(\boldsymbol{\alpha}+\boldsymbol{\beta})=\mathscr{A}(\boldsymbol{\alpha})+\mathscr{A}(\boldsymbol{\beta})$
(2) $\mathscr{A}(k \boldsymbol{\alpha})=k \mathscr{A}(\boldsymbol{\alpha}), \quad \forall k \in K$
则称$\mathscr{A}$为线性空间$V$的一个线性变换。称$\boldsymbol{\beta}$为$\boldsymbol{\alpha}$在线性变换$\mathscr{A}$下的像，记作$\boldsymbol{\beta}=\mathscr{A}$或$\boldsymbol{\beta}=\mathscr{A}(\boldsymbol{\alpha})$

• 特殊的变换
  设$V$是数域$F$上的线性空间，$k$是数域$F$中的一个固定的常数，定义$V$的变换$\mathscr{A}$： $$\mathscr{A}(\boldsymbol{\alpha})=k \boldsymbol{\alpha}, \forall \boldsymbol{\alpha} \in V,$$
  • $\mathscr{A}$为线性变换，称为数乘变换
  • 若$k=1$，称此变换为恒等变换，可记为$\mathscr{A}=\mathrm{id}_{V}$
  • 若$k=0$时，称此变换为零变换，记为$\mathscr{O}$，即$\mathscr{O} \boldsymbol{\alpha}=\mathbf{0}$

值域、核、秩、零度

设$A$为线性空间$V$的线性变换，令

$$\begin{array}{c} \operatorname{Im}(\mathscr{A})=\{\mathscr{A}(\boldsymbol{\xi}) \mid \boldsymbol{\xi} \in V\}, \\ \operatorname{Ker}(\mathscr{A})=\{\boldsymbol{\xi} \in V \mid \mathscr{A}(\boldsymbol{\xi})=0\}, \end{array}$$

则称$\operatorname{Im}(\mathscr{A})$为线性变换$\mathscr{A}$的值域，$\operatorname{Ker}(\mathscr{A})$为线性变换$\mathscr{A}$的核。
令

$$\begin{array}{c} r(\mathscr{A})=\operatorname{dim}(\operatorname{Im}(\mathscr{A})) \\ r(\operatorname{Ker}(\mathscr{A}))=\operatorname{dim}(\operatorname{Ker}(\mathscr{A})) \end{array}$$

则称$r(\mathscr{A})$为线性变换$\mathscr{A}$的秩，$r(\operatorname{Ker}(\mathscr{A}))$为线性变换$\mathscr{A}$的零度

• 一定有$\mathbf{0}\in \operatorname{Ker}(\mathscr{A})$
• $\operatorname{Ker}(\mathscr{A})=\{\mathbf{0}\}\Leftrightarrow \mathscr{A}$是单射$\Leftrightarrow$ $\operatorname{Im}(\mathscr{A})=V$ $\Leftrightarrow$ $\mathscr{A}$是满射

线性变换的纯量乘积

设$V$为数域$F$上的线性空间，$k \in F$,$\mathscr{A}$与$\mathscr{B}$为$V$的两个线性变换，令

$$\begin{aligned} (\mathscr{A}+\mathscr{B})(\boldsymbol{\alpha}) &=\mathscr{A}(\boldsymbol{\alpha})+\mathscr{B}(\boldsymbol{\alpha}), & & \forall \boldsymbol{\alpha} \in V, \\ (k \mathscr{A})(\boldsymbol{\alpha}) &=k(\mathscr{A}(\boldsymbol{\alpha})), & & \forall k \in F, \forall \boldsymbol{\alpha} \in V, \\ (\mathscr{A} \mathscr{B})(\boldsymbol{\alpha}) &=\mathscr{A}(\mathscr{B}(\boldsymbol{\alpha})), & & \forall \boldsymbol{\alpha} \in V, \end{aligned}$$

则称$\mathscr{A}+\mathscr{B}$为线性变换$\mathscr{A}$与$\mathscr{B}$的和，$k \mathscr{A}$为数$k$与线性变换$\mathscr{A}$的纯量乘积，$\mathscr{A}\mathscr{B}$为线性变换$\mathscr{A}$与$\mathscr{B}$的积

• 定理：若$V$为数域$F$上的线性空间，$k \in F$,$ \mathscr{A}$与$\mathscr{B}$为$V$中的两个线性变换，则$\mathscr{A}+\mathscr{B}$,$k \mathscr{A}$与$\mathscr{A}\mathscr{B}$都是$V$的线性变换

线性变换的性质

若$\mathscr{A}$是数域$F$上的线性空间$V$的线性变换，则

• $\mathscr{A}(\mathbf{0})=\mathbf{0}, \mathscr{A}(-\boldsymbol{\alpha})=-\mathscr{A}(\boldsymbol{\alpha})$
• 线性变换保持线性关系式不变，即对$\forall \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m} \in V$,$ k_{1}, k_{2}, \cdots, k_{m} \in F$有 $$\mathscr{A}\left(k_{1} \boldsymbol{\alpha}_{1}+k_{2} \boldsymbol{\alpha}_{2}+\cdots+k_{m} \boldsymbol{\alpha}_{m}\right)=k_{1} \mathscr{A}\left(\boldsymbol{\alpha}_{1}\right)+k_{2} \mathscr{A}\left(\boldsymbol{\alpha}_{2}\right)+\cdots+k_{m} \mathscr{A}\left(\boldsymbol{\alpha}_{m}\right)$$ 即 $$\mathscr{A}[\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}\right) \boldsymbol{k}]=\left(\mathscr{A} \boldsymbol{\alpha}_{1}, \mathscr{A} \boldsymbol{\alpha}_{2}, \cdots, \mathscr{A}\boldsymbol{\alpha}_{m}\right) \boldsymbol{k}$$ 其中$\boldsymbol{k}=\left(k_{1}, k_{2}, \cdots, k_{m}\right)^{\mathrm{T}}$
• 推论：线性变换$\mathscr{A}$将$V$中线性相关的向量组$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{m}$变换到线性相关的向量组

线性变换在给定基下的矩阵

设$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$是$n$维线性空间$V$的一组基，$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2},\cdots, \boldsymbol{\varepsilon}_{n}$在线性变换$\mathscr{A}$下的像分别为

$$\left\{\begin{array}{c} \mathscr{A}\left(\boldsymbol{\varepsilon}_{1}\right)=a_{11} \boldsymbol{\varepsilon}_{1}+a_{21} \boldsymbol{\varepsilon}_{2}+\cdots+a_{n 1} \boldsymbol{\varepsilon}_{n} \\ \mathscr{A}\left(\boldsymbol{\varepsilon}_{2}\right)=a_{12} \boldsymbol{\varepsilon}_{1}+a_{22} \boldsymbol{\varepsilon}_{2}+\cdots+a_{n 2} \boldsymbol{\varepsilon}_{n} \\ \vdots \\ \mathscr{A}\left(\boldsymbol{\varepsilon}_{n}\right)=a_{1 n} \boldsymbol{\varepsilon}_{1}+a_{2 n} \boldsymbol{\varepsilon}_{2}+\cdots+a_{n n} \boldsymbol{\varepsilon}_{n} \end{array}\right.$$

利用分块矩阵乘法，可将上式表示为如下形式：

$$\mathscr{A}\left(\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}\right)=\left(\mathscr{A}\left(\boldsymbol{\varepsilon}_{1}\right), \mathscr{A}\left(\boldsymbol{\varepsilon}_{2}\right), \cdots, \mathscr{A}\left(\boldsymbol{\varepsilon}_{n}\right)\right)=\left(\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}\right) A,$$

则称矩阵

$$\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}=\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right)$$

为线性变换$\mathscr{A}$在基$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$下的矩阵

• 定理：设$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$是数域$K$上的$n$维线性空间$V$的一组基，$\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$是一个$n$阶方阵，那么必存在唯一的线性变换$\mathscr{A}$，它在基$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$下的矩阵为$\boldsymbol{A}$

• 定理：设$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$是$n$维线性空间$V$的一组基，那么$V$中所有的线性变换$\mathscr{A}$与所有的$n$阶方阵$\boldsymbol{A}$之间存在一一对应的关系，这种关系由

  $$\left(\mathscr{A}\left(\boldsymbol{\varepsilon}_{1}\right), \mathscr{A}\left(\boldsymbol{\varepsilon}_{2}\right), \cdots, \mathscr{A}\left(\boldsymbol{\varepsilon}_{n}\right)\right)=\left(\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}\right) \boldsymbol{A}$$

  确定

线性变换在不同基下矩阵间的关系

设$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$和$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}$是$n$维线性空间$V$的两组基，$V$的线性变换$\mathscr{A}$在这两组基下的矩阵分别为$\boldsymbol{A}$和$\boldsymbol{B}$，且从$\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \cdots, \boldsymbol{\varepsilon}_{n}$到$\boldsymbol{\eta}_{1}, \boldsymbol{\eta}_{2}, \cdots, \boldsymbol{\eta}_{n}$的过渡矩阵为$\boldsymbol{C}$，那么

$$\boldsymbol{B}=\boldsymbol{C}^{-1} \boldsymbol{A} \boldsymbol{C}$$

第五章 矩阵的相似对角化

特征值、特征向量的定义

设$\boldsymbol{A}$为数域$F$上的一个$n$阶方阵，$\lambda \in F$，$\boldsymbol{\alpha}$为$F$上的$n$维非零列向量. 若

$$\boldsymbol{A} \boldsymbol{\alpha}=\lambda \boldsymbol{\alpha},$$

则称$\lambda$为方阵$\boldsymbol{A}$的一个特征值，$\boldsymbol{\alpha}$为$\boldsymbol{A}$的对应于特征值$\lambda$的特征向量

几何重数

特征子空间$V_{\lambda_0}$的维数称为特征值$\lambda_0$的几何重数，几何重数一定 $>0$

特征多项式与特征方程

设数域 $F$ 上的 $n$ 阶方阵 $\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$ ，称

$$f(\lambda)=|\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{cccc} \lambda-a_{11} & -a_{12} & \cdots & -a_{1 n} \\ -a_{21} & \lambda-a_{22} & \cdots & -a_{2 n} \\ \vdots & \vdots & & \vdots \\ -a_{n 1} & -a_{n 2} & \cdots & \lambda-a_{n n} \end{array}\right|$$

为矩阵 $\boldsymbol{A}$ 的特征多项式，$|\lambda \boldsymbol{E}-\boldsymbol{A}|=0$ 叫作 $\boldsymbol{A}$ 的特征方程
由 $n$ 阶行列式的定义可知，上面行列式的展开式 $f(\lambda)$ 为 $\lambda$ 的 $n$ 次多项式 $f(\lambda)=\lambda^{n}-\left(a_{11}+a_{22}+\cdots+a_{n n}\right) \lambda^{n-1}+\cdots+(-1)^{n}|\boldsymbol{A}|$
由代数基本定理，$f(\lambda)$ 在复数域内恰有 $n$ 个根 (重根按重数计算)，所以 $n$ 阶方阵在复数域内必有 $n$ 个特征值 (重根按重数计算)

设 $n$ 阶方阵 $\boldsymbol{A}$ 的特征多项式在复数域内的分解式为 $|\lambda \boldsymbol{E}-\boldsymbol{A}|=\left(\lambda-\lambda_{1}\right)^{n_{1}}\left(\lambda-\lambda_{2}\right)^{n_{2}} \cdots\left(\lambda-\lambda_{s}\right)^{n_{s}}$
其中 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$ 两两不同， $n_{1}+n_{2}+\cdots+n_{s}=n$ .称特征值 $\lambda_{i}$ 为此特征多项式的 $n_{i}$ 重根，$n_{i}$ 叫作 $\lambda_{i}$ 的代数重数， $i=1,2, \cdots ,s$. 特别地，代数重数为 $1$ 的特征值也称为单特征值或特征多项式的单根

特征值的性质

• $\lambda$是矩阵$\boldsymbol{A}$的特征值的充分必要条件为$|\lambda\boldsymbol{E}-\boldsymbol{A}|=0$
• $r(\boldsymbol{A})=r$，则 $\boldsymbol{A}$ 至少有 $n-r$ 个特征值为 $0$
• 若$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$是对应于某个特征值$\lambda_0$的任意$s$个特征向量，则它们的任一非零线性组合$\sum_{i=1}^s k_i \boldsymbol{\alpha}_i$也是$\boldsymbol{A}$的对应于$\lambda_0$的特征向量
• 对应于某个特征值$\lambda_0$的全体特征向量连同零向量一起组成$n$维向量空间$F^n$的一个子空间，它是齐次线性方程组$(\lambda_0\boldsymbol{E}-\boldsymbol{A})\boldsymbol{X}=\mathbf{0}$的解空间，称之为矩阵$\boldsymbol{A}$的对应于特征值$\lambda_0$的特征子空间，记为$V_{\lambda_0}$
• 对角矩阵的特征值就是对角线上的所有元素，同阶的单位矩阵的列向量可分别看作是它们所对应的一个特征向量
• 对行和相等的方阵，这个行和一定是它的一个特征值，而分量均为1的列向量必为这个特征值所对应的一个特征向量
• 如果矩阵可以对角化，那么非零特征值的个数就等于矩阵的秩；如果矩阵不可以对角化，不一定成立。
• 设 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ 为 $n$ 阶方阵 $\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$ 的 $n$ 个特征值，则 $$\begin{array}{c} \sum_{j=1}^{n} \lambda_{j}=\sum_{i=1}^{n} a_{i i}=\operatorname{tr}(\boldsymbol{A}) \\ \prod_{j=1}^{n} \lambda_{j}=|\boldsymbol{A}| \end{array}$$
• 方阵$\boldsymbol{A}$与$\boldsymbol{A}^{\mathrm{T}}$有相同的特征多项式和特征值
• 设 $\lambda$ 为方阵 $\boldsymbol{A}$ 的特征值，$\boldsymbol{\alpha}$ 为对应于 $\lambda$ 的特征向量，则
  • $k \lambda$ 是方阵 $k \boldsymbol{A}$ 的特征值，$\boldsymbol{\alpha}$ 也为 $k \boldsymbol{A}$ 的对应于特征值 $k \lambda$ 的特征向量，其中 $k$ 为任意常数
  • $\lambda^{m}$ 是 $\boldsymbol{A}^{m}$ 的特征值， $\boldsymbol{\alpha}$ 也为方阵 $\boldsymbol{A}^{m}$ 的对应于特征值 $\lambda^{m}$ 的特征向量，其中 $m$ 为任意正整数
  • $g(\lambda)$ 是 $g(\boldsymbol{A})$ 的特征值，$\boldsymbol{\alpha}$ 也是 $g(\boldsymbol{A})$ 的对应于特征值 $g(\lambda)$ 的特征向量，其中 $$g(x)=a_{m} x^{m}+a_{m-1} x^{m-1}+\cdots+a_{1} x+a_{0}$$ 为数域 $F$ 上的多项式，$m$ 为正整数
  • $\lambda+1$ 是方阵 $\boldsymbol{A}+\boldsymbol{E}$ 的特征值，$\boldsymbol{\alpha}$ 也为 $\boldsymbol{A}+\boldsymbol{E}$ 的对应于特征值 $\lambda+1$ 的特征向量
• 若 $n$ 阶方阵 $\boldsymbol{A}$ 的 $n$ 个特征值为 $\lambda_{1} , \lambda_{2}, \cdots, \lambda_{n}$，则关于 $\boldsymbol{A}$ 的多项式函数得到的矩阵 $g(\boldsymbol{A})$ 的全部特征值为 $g\left(\lambda_{1}\right), g\left(\lambda_{2}\right), \cdots, g\left(\lambda_{n}\right)$ ，且 $g(\lambda)$ 的代数重数和几何重数分别大于或等于 $\lambda$ 的代数重数和几何重数
• $n$阶方阵 $\boldsymbol{A}$ 可逆的充分必要条件为 $\boldsymbol{A}$ 的 $n$ 个特征值全不为零
• 设 $\lambda$ 为可逆矩阵 $\boldsymbol{A}$ 的特征值，$\boldsymbol{\alpha}$ 为$A$的对应于 $\lambda$ 的特征向量，则
  • $\frac{1}{\lambda}$为其逆矩阵$\boldsymbol{A}^{-1}$的特征值，且$\boldsymbol{\alpha}$是$\boldsymbol{A}^{-1}$的对应于特征值$\frac{1}{\lambda}$的特征向量
  • $\frac{1}{\lambda} \cdot|\boldsymbol{A}|$ 为其伴随矩阵 $\boldsymbol{A}^{\star}$ 的特征值，$\boldsymbol{\alpha}$也是$A^{\star}$的对应于特征值 $\frac{1}{\lambda} \cdot|\boldsymbol{A}|$的特征向量
• 设$\lambda_0$是方阵$\boldsymbol{A}$ 的一个特征值，则它的几何重数小于等于代数重数
• 设$\lambda_0$是方阵$\boldsymbol{A}$ 的一个单特征值，则$\boldsymbol{A}$的对应于$\lambda_0$的线性无关的特征向量有且仅有一个
• 设 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$ 为 $n$ 阶方阵 $\boldsymbol{A}$ 的 $s$ 个不同特征值，$\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$ 分别是对应它们的特征向量，则 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{s}$ 线性无关
  • 推论：$\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$ 为 $n$ 阶方阵 $\boldsymbol{A}$ 的 $s$ 个不同特征值，$\boldsymbol{\alpha}_{i 1} , \alpha_{i 2}, \cdots, \alpha_{i r_{i}}$ 为对应于特征值$\lambda_{i}$ 的 $r_{i}$ 个线性无关的特征向量，$1 \leqslant i \leqslant s$，则向量组 $$\boldsymbol{\alpha}_{11}, \boldsymbol{\alpha}_{12}, \cdots, \boldsymbol{\alpha}_{1 r_{1}} ; \boldsymbol{\alpha}_{21}, \boldsymbol{\alpha}_{22}, \cdots, \boldsymbol{\alpha}_{2 r_{2}} ; \cdots ; \boldsymbol{\alpha}_{s 1}, \boldsymbol{\alpha}_{s 2}, \cdots, \boldsymbol{\alpha}_{s r_{3}}$$ 线性无关.

相似矩阵

设$\boldsymbol{A}$与$\boldsymbol{B}$都是数域$F$上的$n$阶方阵，若存在$F$上的$n$阶可逆矩阵$\boldsymbol{P}$使得

$$\boldsymbol{P}^{-1} \boldsymbol{A P}=\boldsymbol{B},$$

则称方阵$\boldsymbol{A}$与$\boldsymbol{B}$相似，记作$\boldsymbol{A} \sim \boldsymbol{B}$. 特别地，若$\boldsymbol{A}$相似于对角阵，则称$\boldsymbol{A}$可对角化.

方阵的相似关系是一种等价关系，即方阵的相似具有:

• 反身性. 设 $\boldsymbol{A} \in F^{n \times n}$，则 $\boldsymbol{A} \sim \boldsymbol{A}$
• 对称性. 设 $\boldsymbol{A}, \boldsymbol{B} \in F^{n \times n}$，若 $\boldsymbol{A} \sim \boldsymbol{B}$，则 $\boldsymbol{B} \sim \boldsymbol{A}$
• 传递性. 设 $\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C} \in F^{n \times n}$，若 $\boldsymbol{A} \sim \boldsymbol{B}$ 且 $\boldsymbol{B} \sim \boldsymbol{C}$ ，则 $\boldsymbol{A} \sim \boldsymbol{C}$

相似矩阵的性质

• 相似矩阵有相同的秩
• 相似矩阵有相同的特征多项式、特征值、行列式、迹
• $n$ 阶实对称矩阵 $\boldsymbol{A},\boldsymbol{B}$ 有完全相同的特征值，则 $\boldsymbol{A}$ 与 $\boldsymbol{B}$ 相似
• 设$\boldsymbol{A} \sim \boldsymbol{B}$，且$A$可逆，则$B$可逆，且$\boldsymbol{A}^{-1} \sim \boldsymbol{B}^{-1}$
• 设 $\boldsymbol{A} \sim \boldsymbol{B}$，则
  • $\boldsymbol{A} \sim \boldsymbol{B}$
  • $k \boldsymbol{A} \sim k \boldsymbol{B}, k \in F$
  • $\boldsymbol{A}^{m} \sim \boldsymbol{B}^{m}$，其中 $m$ 是任意正整数
  • $g(\boldsymbol{A}) \sim g(\boldsymbol{B})$，其中 $$g(x)=a_{m} x^{m}+a_{m-1} x^{m-1}+\cdots+a_{1} x+a_{0}$$ 为数域 $F$ 上的 $m$ 次多项式，$m$ 为非负整数
• 设$\boldsymbol{A}$与$\boldsymbol{B}$为数域$F$上的分块对角阵 $$\boldsymbol{A}=\left(\begin{array}{llll} \boldsymbol{A}_{1} & & & \\ & \boldsymbol{A}_{2} & & \\ & & \ddots & \\ & & & \boldsymbol{A}_{t} \end{array}\right), \boldsymbol{B}=\left(\begin{array}{llll} \boldsymbol{B}_{1} & & & \\ & \boldsymbol{B}_{2} & & \\ & & \ddots & \\ & & & \boldsymbol{B}_{t} \end{array}\right) \text {. }$$ 此处, $\boldsymbol{A}_{i}$ 与 $\boldsymbol{B}_{i}$ 都是 $n_{i}$ 阶方阵, $1 \leqslant i \leqslant t$. 若对所的 $i$,$1 \leqslant i \leqslant t$, $\boldsymbol{A}_{i}$ 与 $\boldsymbol{B}_{i}$ 相似，则 $\boldsymbol{A}$ 与 $\boldsymbol{B}$ 相似
• 设 $A=\left(a_{i j}\right)_{n \times n}$ 为复数域 $\mathbb{C}$ 上的 $n$ 阶方阵，则存在复数域 $\mathbb{C}$ 上的上三角矩阵 $\boldsymbol{B}$ 与矩阵 $\boldsymbol{A}$ 相似.

矩阵相似对角阵的条件

设 $A$ 为复数域 $\mathbb{C}$ 上的 $n$ 阶方阵, 则 $A$ 相似于对角阵的充分必要条件是 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量

• 推论：若 $n$ 阶方阵 $\boldsymbol{A}$ 有 $n$ 个不同的特征值，则 $\boldsymbol{A}$ 必可对角化.
• 推论：设 $n$ 阶方阵 $\boldsymbol{A}$ 有 $s$ 个不同的特征值 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$. 对$1\leqslant i \leqslant s$,$\lambda_{i}$ 的代数重数与几何重数分别为 $n_{i}$ 与 $m_{i}$, 则方阵 $\boldsymbol{A}$ 相似于对角阵的充分必要条件为 $$m_{i}=n_{i}, i=1,2, \cdots, s .$$

判断是否可对角化及对角化方法

判断一个方阵 $\boldsymbol{A}_{n}$ 是否相似于对角阵及求可逆矩阵 $\boldsymbol{P}$，使得 $\boldsymbol{P}^{-1} \boldsymbol{A P}$ 为对角阵的一般步骤为：

1. 求出方阵 $\boldsymbol{A}$ 的所有特征值 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$, 它们的代数重数分别为 $n_{1}, n_{2}, \cdots, n_{s}, \sum_{j=1}^{s} n_{j}=n$
2. 对每个特征值 $\lambda_{j}$，计算 $r\left(\lambda_{j} \boldsymbol{E}-\boldsymbol{A}\right)$，若 $$r\left(\boldsymbol{\lambda}_{j} \boldsymbol{E}-\boldsymbol{A}\right)=n-n_{j}, j=1,2, \cdots, s,$$ 则 $\boldsymbol{A}$ 可对角化；否则，不能对角化
3. 在可对角化的情况下，对每个 $\lambda_{j}$，求出齐次线性方程组 $\left(\lambda_{j} \boldsymbol{E}-\boldsymbol{A}\right) \boldsymbol{x}=\mathbf{0}$ 的基础解系 $$\boldsymbol{\alpha}_{j 1}, \boldsymbol{\alpha}_{j 2}, \cdots, \boldsymbol{\alpha}_{j n_{j}}, j=1,2, \cdots, s$$
4. 令 $$\boldsymbol{P}=\left(\boldsymbol{\alpha}_{11}, \boldsymbol{\alpha}_{12}, \cdots, \boldsymbol{\alpha}_{1 n_{1}}, \cdots, \boldsymbol{\alpha}_{s 1}, \boldsymbol{\alpha}_{s 2}, \cdots, \boldsymbol{\alpha}_{s n_{s}}\right),$$ 则 $\boldsymbol{P}$ 可逆，且有 $$\boldsymbol{P}^{-1} \boldsymbol{A P}=\boldsymbol{\Lambda}=\operatorname{diag}(\underbrace{\lambda_{1}, \cdots, \lambda_1}_{n_{1} \text{个}}, \underbrace{\lambda_{2}, \cdots, \lambda_{2}}_{n_{2} \text{个}} \cdots, \underbrace{\lambda_{s}, \cdots, \lambda_{s}}_{n_{s} \text{个}})$$

一个结论：设 $\boldsymbol{A}$ 是一个 $n$ 阶方阵，满足 $(\boldsymbol{A}-a \boldsymbol{E})(\boldsymbol{A}-b \boldsymbol{E})=\boldsymbol{O}$，其中 $a \neq b$. 则 $\boldsymbol{A}$ 相似于对角矩阵.

实对称矩阵的特征值与特征向量

• 实对称矩阵的特征值全是实数
• 实对称矩阵的属于不同特征值的实特征向量正交

实对称矩阵正交相似对角阵

设 $\boldsymbol{A}$ 为 $n$ 阶实对称矩阵, 则存在 $n$ 阶正交矩阵 $\boldsymbol{Q}$, 使得

$$\boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}=\varLambda$$

其中

$$\boldsymbol{\varLambda}=\left(\begin{array}{llll} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n} \end{array}\right), \lambda_{1}, \lambda_{2}, \cdots, \lambda_{n} \text { 为 } \boldsymbol{A} \text { 的特征值. }$$

• 推论：n阶实对称矩阵必有n个线性无关的特征向量
• 推论：n阶实对称矩阵的每个特征值的几何重数必等于它的代数重数
• 推论：n阶实对称矩阵的不同特征值对应的特征向量正交

求实对称矩阵正交相似对角阵的方法

实对称矩阵 $\boldsymbol{A}$ 必能正交相似于对角阵. 找出正交矩阵 $\boldsymbol{Q}$ 使得 $\boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}=\Lambda$ (对角阵) 的方法如下.

1. 求出实对称矩阵 $\boldsymbol{A}$ 的全部特征值 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{s}$，它们的代数重数分别为 $n_{1}, n_{2}, \cdots, n_{s}, \sum_{i=1}^{s} n_{i}=n$
2. 对每个 $\lambda_{i}$，求出齐次线性方程组 $\left(\lambda_{i} E-\boldsymbol{A}\right) \boldsymbol{x}=\mathbf{0}$ 的基础解系 $$\boldsymbol{\alpha}_{i 1}, \boldsymbol{\alpha}_{i 2}, \cdots, \boldsymbol{\alpha}_{i n_{i}}, \quad i=1,2, \cdots, s$$
3. 对 $\boldsymbol{\alpha}_{i 1}, \boldsymbol{\alpha}_{i 2}, \cdots, \boldsymbol{\alpha}_{i n_{i}}$ 正交化、单位化得 $\boldsymbol{\varepsilon}_{i 1}, \boldsymbol{\varepsilon}_{i 2}, \cdots, \boldsymbol{\varepsilon}_{i n_{i}}, i=1,2,\cdots, s$ ，即 $$\boldsymbol{\varepsilon}_{11}, \boldsymbol{\varepsilon}_{12}, \cdots, \boldsymbol{\varepsilon}_{1 n_{1}}, \cdots, \boldsymbol{\varepsilon}_{s 1}, \boldsymbol{\varepsilon}_{s 2}, \cdots, \boldsymbol{\varepsilon}_{s n_{s}}$$ 为两两正交的单位特征向量
4. 令 $$\boldsymbol{Q}=\left(\boldsymbol{\varepsilon}_{11}, \boldsymbol{\varepsilon}_{12}, \cdots, \boldsymbol{\varepsilon}_{1 n_{1}}, \cdots, \boldsymbol{\varepsilon}_{s 1}, \boldsymbol{\varepsilon}_{s 2}, \cdots, \boldsymbol{\varepsilon}_{s n_{s}}\right),$$ 则 $\boldsymbol{Q}$ 为正交矩阵，且有 $$\boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{\Lambda}=\operatorname{diag}(\underbrace{\lambda_{1}, \cdots, \lambda_{1}}_{n_{1} \text{个}}, \underbrace{\lambda_{2}, \cdots, \lambda_{2}}_{n_{2} \text{个}}, \cdots, \underbrace{\lambda_{s}, \cdots, \lambda_{s}}_{n_{s} \text{个}}) .$$

第六章 实二次型

二次型相关定义

称含 $n$ 个变量 $x_{1}, x_{2}, \cdots, x_{n}$ 的二次齐次函数

$$\begin{aligned} f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=& a_{11} x_{1}^{2}+2 a_{12} x_{1} x_{2}+\cdots+2 a_{1 n} x_{1} x_{n}+\\ & a_{22} x_{2}^{2}+\cdots+2 a_{2 n} x_{2} x_{n}+\cdots+a_{n n} x_{n}^{2} \end{aligned}$$

为一个 $n$ 元二次型，简称二次型. 当系数 $a_{i j}$ 为实数时，称为一个实二次型；当系数 $a_{i j}$ 为复数时，称为一个复二次型
只含平方项的二次型

$$f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=a_{11} x_{1}^{2}+a_{22} x_{2}^{2}+\cdots+a_{n n} x_{n}^{2}$$

称为标准二次型
如果标准二次型中各项的系数为 $1,-1$ 或 $0$，且系数为 $1$ 的都在前面，例如

$$f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=x_{1}^{2}+x_{2}^{2}+\cdots+x_{p}^{2}-x_{p+1}^{2}-\cdots-x_{r}^{2} \quad(r \leqslant n)$$

则称其为规范二次型
本章我们只讨论实二次型，除非特别声明
设 $a_{i j}=a_{j i}(i, j=1,2, \cdots, n)$，则二次型可表示为

$$\begin{aligned} f=& a_{11} x_{1}^{2}+a_{12} x_{1} x_{2}+\cdots+a_{1 n} x_{1} x_{n}+a_{21} x_{2} x_{1}+a_{22} x_{2}^{2}+\cdots+\\ & a_{2 n} x_{2} x_{n}+\cdots+a_{n 1} x_{n} x_{1}+a_{n 2} x_{n} x_{2}+\cdots+a_{n n} x_{n}^{2} \\ =& \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j} x_{i} x_{j} . \end{aligned}$$

又设矩阵

$$\boldsymbol{A}=\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right), \quad \boldsymbol{x}=\left(\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right)$$

则 $\boldsymbol{A}$ 为实对称矩阵，且

$$f=\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j} x_{i} x_{j}=\boldsymbol{x}^{T} \boldsymbol{A} \boldsymbol{x}$$

我们称上式为二次型 $f$ 的矩阵表示式. 由上式可知，二次型 $f$ 与实对称矩阵 $\boldsymbol{A}$ 一一对应. 称实对称阵 $\boldsymbol{A}$ 为二次型 $f$ 的 矩阵. 又称 $\boldsymbol{A}$ 的秩 $r(\boldsymbol{A})$ 为 $f$ 的秩，记作 $r(f)$，即

$$r(f)=r(\boldsymbol{A})$$

标准二次型和规范二次型的矩阵，分别为如下对角矩阵 $\boldsymbol{A}_{1}$ 和 $\boldsymbol{A}_{2}$ ：

$$\boldsymbol{A}_{1}=\left(\begin{array}{cccc} a_{11} & & & \\ & a_{22} & & \\ & & \ddots & \\ & & & a_{n n} \end{array}\right), \boldsymbol{A}_{2}=\left(\begin{array}{lll} \boldsymbol{E}_{p} & & \\ & & -\boldsymbol{E}_{r-p} & \\ & & & & \boldsymbol{O} \end{array}\right)$$

其中 $r=r\left(\boldsymbol{A}_{2}\right)=r(f)$

二次型的非奇异线性替换

设$\boldsymbol{x},\boldsymbol{y}$为$n$维向量，$n$阶方阵$\boldsymbol{P}$为可逆矩阵，称

$$\boldsymbol{x}=\boldsymbol{Py}$$

为非奇异（非退化）的线性替换

合同的定义和性质

设 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 为 $n$ 阶方阵，若存在可逆矩阵 $\boldsymbol{P}$，使 $\boldsymbol{P}^{\mathrm{T}} \boldsymbol{A P}=\boldsymbol{B}$，则称矩阵 $\boldsymbol{A}$ 与 $\boldsymbol{B}$ 合同
由定义，可知矩阵的合同关系有如下性质：

• 反身性：$\boldsymbol{A}$ 合同于 $\boldsymbol{A}$
• 对称性：若 $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$，则 $\boldsymbol{B}$ 也合同于 $\boldsymbol{A}$
• 传递性：若 $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$，$\boldsymbol{B}$ 又合同于 $\boldsymbol{C}$，则 $\boldsymbol{A}$ 也合同于 $\boldsymbol{C}$
• 若 $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$，则 $r(\boldsymbol{A})=r(\boldsymbol{B})$
• 若 $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$ 且 $\boldsymbol{A}$ 为对称阵，则 $\boldsymbol{B}$ 也是对称阵
  定理：一个二次型 $f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A x}$ 经非奇异线性替换 $\boldsymbol{x}=\boldsymbol{P y}$ 仍变为一个二次型 $f=\boldsymbol{y}^{\mathrm{T}}\left(\boldsymbol{P}^{\mathrm{T}} \boldsymbol{A P}\right) \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{y}$，且它们的矩阵合同

化二次型为标准二次型的方法

任何一个二次型 $f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$ 必存在正交线性替换 $\boldsymbol{x}= \boldsymbol{Q y}$，$\boldsymbol{Q}$ 为正交矩阵，使得新变量的二次型 $\boldsymbol{y}^{\mathrm{T}}\left(\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}\right) \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{\Lambda} \boldsymbol{y}$ 为标准二次型. 即

$$f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x} \stackrel{\boldsymbol{x}=\boldsymbol{Q} \boldsymbol{y}}{=} \lambda_{1} \boldsymbol{y}_{1}^{2}+\lambda_{2} \boldsymbol{y}_{2}^{2}+\cdots+\lambda_{n} \boldsymbol{y}_{n}^{2},$$

其中 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ 是实对称矩阵 $\boldsymbol{A}$ 的特征值.

设二次型$f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$，则存在非奇异线性替换$\boldsymbol{x}= \boldsymbol{P y}$ 化 $f$ 为标准二次型

惯性定理

任何实二次型必存在非奇异线性替换化二次型为规范标准形，且规范标准形是唯一的。

设二次型 $f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$, $r(f)=r$ ，经非奇异线性替换化 $f$ 为标准形. 若 $f$ 的标准形有 $p$ 个正项，则称 $p$ 为二次型 $f$ 或实对称矩阵 $\boldsymbol{A}$ 的正惯性指数. 又称 $q=r-p$ 和 $s=p-q$ 分别为二次型 $f$ 或实对称矩阵 $\boldsymbol{A}$ 的负惯性指数和符号差.

• 推论：任何实对称矩阵 $A_{n}$ 都合同于对角矩阵 $$\operatorname{diag}(\underbrace{1, \cdots, 1}_{p \text{个}}, \underbrace{-1, \cdots,-1}_{r-p \text{个}}, \underbrace{0, \cdots, 0}_{n-r \text{个}})=\left(\begin{array}{c} \boldsymbol{E}_{p}&& \\ &-\boldsymbol{E}_{r-p}& \\ &&\mathbf{0} \end{array}\right)_{n}$$ 其中 $r=r(\boldsymbol{A})$，$p$ 为 $\boldsymbol{A}$ 的正惯性指数.
• 推论：两个 $n$ 元二次型 $f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$ 与 $g=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{y}$ 有相同的秩及正惯性指数的充要条件为存在非奇异线性替换 $\boldsymbol{x}=\boldsymbol{P y}$，使 $$f=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x} \stackrel{\boldsymbol{x}=\boldsymbol{P} \boldsymbol{y}}{=} \boldsymbol{y}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{y}=g$$
• 推论：$n$ 阶实对称矩阵 $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$ 的充要条件为 $r(\boldsymbol{A})=r(\boldsymbol{B})$，且 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 的正惯性指数相等

正定二次型与正定矩阵

设 $n$ 元二次型

$$f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x},$$

若对任意非零向量 $x_{0}=\left(c_{1}, c_{2}, \cdots, c_{n}\right)^{\mathrm{T}}$, 都有

$$f\left(c_{1}, c_{2}, \cdots, c_{n}\right)=\boldsymbol{x}_{0}^{\mathrm{T}} \boldsymbol{A x}_{0}>0,$$

则称二次型 $f$ 为正定二次型，并称其矩阵 $\boldsymbol{A}$ 为正定矩阵

$n$ 个变量的标准二次型 $f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=k_{1} x_{1}^{2}+k_{2} x_{2}^{2}+ \cdots+k_{n} x_{n}^{2}$ 正定的充分必要条件为 $k_{i}>0$, $i=1,2, \cdots, n$

实二次型 $f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A x}$ 经非奇异线性替换后其正定性不改变

设 $A$ 为 $n$ 阶实对称矩阵，则下述命题等价：

• $\boldsymbol{A}$ 为正定矩阵
• $\boldsymbol{A}$ 的特征值全大于零
• $\boldsymbol{A}$ 合同于单位矩阵 $\boldsymbol{E}$
• 存在非奇异矩阵 $\boldsymbol{M}$，使得 $\boldsymbol{A}=\boldsymbol{M}^{\mathrm{T}} \boldsymbol{M}$

$n$阶实对称矩阵$\boldsymbol{A}$正定，则$|\boldsymbol{A}|>0$

若实对称矩阵$\boldsymbol{A}$正定，则$\boldsymbol{A}$可逆，$\boldsymbol{A}^{-1}$、$\boldsymbol{A}^{\star}$和$\boldsymbol{A}^m$均正定

若实对称矩阵$\boldsymbol{A},\boldsymbol{B}$正定，$\boldsymbol{A},\boldsymbol{B}$ 相乘可换，则$\boldsymbol{AB}$正定

若 $\boldsymbol{A}$ 正定， $\boldsymbol{A}$ 合同于 $\boldsymbol{B}$ ，则 $\boldsymbol{B}$ 正定

顺序主子式

设矩阵 $\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$，则称由 $\boldsymbol{A}$ 的前 $k$ 行前 $k$ 列构成的 $k$ 阶行列式 $(1 \leqslant k \leqslant n)$

$$\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 k} \\ a_{21} & a_{22} & \cdots & a_{2 k} \\ \vdots & \vdots & & \vdots \\ a_{k 1} & a_{k 2} & \cdots & a_{k k} \end{array}\right|$$

为矩阵 $\boldsymbol{A}$ 的 $k$ 阶顺序主子式

$n$ 元二次型

$$f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j} x_{i} x_{j}$$

是正定二次型的充分必要条件为其矩阵 $\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$ 的各阶顺序主子式全大于零，即

$$\left|a_{11}\right|>0,\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|>0,\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|>0, \cdots,$$ $$\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1, n-1} \\ a_{21} & a_{22} & \cdots & a_{2, n-1} \\ \vdots & \vdots & & \vdots \\ a_{n-1,1} & a_{n-1,2} & \cdots & a_{n-1, n-1} \end{array}\right|>0,\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|>0$$

负定二次型、不定二次型

设 $n$ 元二次型 $f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j} x_{i} x_{j}$ ，若对任意非零列向量 $x_{0}=\left(c_{1}, c_{2}, \cdots, c_{n}\right)^{\mathrm{T}}$ ，都有

$$f\left(c_{1}, c_{2}, \cdots, c_{n}\right)=\boldsymbol{x}_{0}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}_{0}<0(\geqslant 0, \leqslant 0)$$

则称二次型$f$为负定二次型（半正定二次型，半负定二次型），并称其矩阵 $\boldsymbol{A}$ 为负定矩阵（半正定矩阵，半负定矩阵）

矩阵$\boldsymbol{A}$是负定二次型的充要条件是$\boldsymbol{A}$的奇数阶顺序主子式全小于0，偶数阶的顺序主子式全大于0

若存在非零向量 $\boldsymbol{x}_{1}=\left(c_{1}, c_{2}, \cdots, c_{n}\right)^{\mathrm{T}} \neq \mathbf{0}$ 和 $\boldsymbol{x}_{2}=\left(d_{1}, d_{2}, \cdots, d_{n}\right)^{\mathrm{T}} \neq \mathbf{0}$ 使

$$\begin{array}{c} f\left(c_{1}, c_{2}, \cdots, c_{n}\right)=\boldsymbol{x}_{1}^{\mathrm{T}} A \boldsymbol{x}_{1}>0, \\ f\left(d_{1}, d_{2}, \cdots, d_{n}\right)=\boldsymbol{x}_{2}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}_{2}<0, \end{array}$$

则称 $f$ 为不定二次型，并称其矩阵 $\boldsymbol{A}$ 为不定矩阵